problems
modal propositional logic
-
Draw a possible world model that shows that the relevant formula is not true in all worlds of all models of the specified sort.
-
\(\Diamond p \to \Box p\) / euclidean
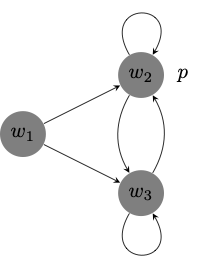
-
\(\Box (\Box p \to p)\) / symmetric
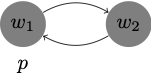
-
\(\Diamond(p \to q) \to (\Diamond p \to \Diamond q)\) / reflexive
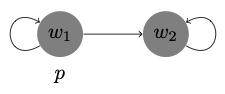
-
\(\Box \Box p \to \Box p\) / transitive
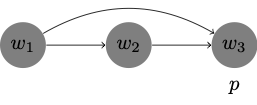
-
\(\Diamond p \to \Box \Diamond p\) / reflexive and transitive
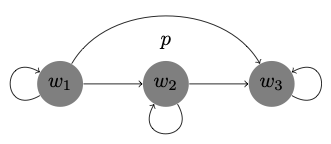
-
-
Justify the claim that no formula of the form \(\Box \Diamond \varphi\) is valid in all frames.
Hint. You should be able to find a model in which all such formulas are in fact false at some world.
Set \(W = \{w_1, w_2\}\) and \(R = \{(w_1, w_2)\}\). Because \(w_2\) is a dead end in the model, we know that every formula of the form \(\Diamond \varphi\) is false at \(w_2\) in every model based on that frame. So, \(\Box \Diamond \varphi\) is never true at \(w_1\), and we conclude that the formula is not valid in the frame just now given.
-
Call a relation \(R\) is serial on \(W\) if, and only if, for all \(u \in W\), there is some \(v\in W\) such that \(uRv\). On the other hand, a relation \(R\) is functional on \(W\) if, and only if, for all \(w, u, v \in W\), if \(wRu\) and \(wRv\), then \(u = v\).
Justify the claims below:
-
\(\Box p \to \Diamond p\) defines the class of serial frames.
We argue that for every frame \((W, R)\), \((W, R) \models \Box p \to \Diamond p\) if, and only if, \(R\) is serial on \(W\).
(\(\Leftarrow\)) Suppose \(R\) is serial on \(W\). We argue that for all \(V\), \((W, R, V) \Vdash \Box p \to \Diamond p\). Fix a valuation \(V\). Now, given \(w \in W\), assume \((W,R, V), w \Vdash \Box p\). Since \(R\) is serial on \(W\), there is some \(u\in W\) such that \(Rwu\). But since \((W,R, V), w \Vdash \Box p\) and \(Rwu\), \((W,R, V), u \Vdash p\) and \((W,R, V), w \Vdash \Diamond p\).
(\(\Rightarrow\)) Suppose \(R\) is not serial on \(W\). That is, there is some \(w\in W\) such that \(\neg Rwu\) for all \(u \in W\). Consider a valuation \(V\) such that \(V(p) = \{u\in W:Rwu\}\). Note that by definition of \(V\), \((W,R, V), w \Vdash \Box p\). However, \((W,R, V), w \Vdash \Diamond p\), since \((W,R, V), u \nVdash p\) for all \(u\in W\) such that \(Rwu\).
-
\(\Diamond p \to \Box p\) defines the class of functional frames.
We argue that for every frame \((W, R)\), \((W, R) \models \Diamond p \to \Box p\) if, and only if, \(R\) is functional on \(W\).
(\(\Leftarrow\)) Suppose \(R\) is functional on \(W\). We argue that for all \(V\), \((W, R, V) \Vdash \Diamond p \to \Box p\). Fix a valuation \(V\). Now, given \(w \in W\), assume \((W,R, V), w \Vdash \Diamond p\). That means that there is some \(u \in W\) such that \((W,R, V), u \Vdash p\). Since \(R\) is functional on \(W\), there is at most one such \(u\in W\) such that \(Rwu\). But since \((W,R, V), u \Vdash p\), we conclude that \((W,R, V), w \Vdash \Box p\).
(\(\Rightarrow\)) Suppose \(R\) is not functional on \(W\). That is, there are some \(w, u, v\in W\) such that \(Rwu\) and \(Rwv\) and \(u \neq v\). Consider a valuation \(V\) such that \(V(p) = \{u\}\). By definition of \(V\), \((W,R, V), u \Vdash p\) and \((W,R, V), w \Vdash \Diamond p\). However, \((W,R, V), v \nVdash p\), which means that \((W,R, V), w \nVdash \Box p\).
-
-
Find a modal formula to define the class of identity frames, that is, fames of the form \((W, R)\), where \(R = \{(u,u): u \in W\}\).
The formula \(p \leftrightarrow \Box p\) defines the class of identity frames.
We argue that for every frame \((W, R)\), \((W, R) \models p \leftrightarrow \Box p\) if, and only if, \(R\) is the identity relation on \(W\).
(\(\Leftarrow\)) Suppose \(R\) is the identity relation on \(W\). We argue that for all \(V\), \((W, R, V) \Vdash p \leftrightarrow \Box p\). Fix a valuation \(V\). Now, given \(w \in W\), we argue that \((W, R, V), w \Vdash p \leftrightarrow \Box p\). There are two cases to consider.
If \(w \in V(p)\), then \((W, R, V), w \Vdash p\) and \((W, R, V), w \Vdash \Box p\). The reason for the latter is that for all \(u \in W\), \(Rwu\) only if \(u=w\).
If \(w \notin V(p)\), then \((W, R, V), w \nVdash p\) and \((W, R, V), w \nVdash \Box p\). The reason for the latter is that \(Rww\) and \((W, R, V), w \nVdash p\).
(\(\Rightarrow\)) Suppose \(R\) is not the identity relation on \(W\). That is, there are some \(w, u\in W\) such that \(Rwu\) and \(w \neq u\). Consider a valuation \(V\) such that \(V(p) = \{w\}\). Note that by definition of \(V\), \((W,R, V), w \Vdash p\) and \((W,R, V), u \nVdash p\). Therefore, since \(Rwu\), \((W,R, V), w \nVdash \Box p\), which means that \((W,R, V), w \nVdash p \leftrightarrow \Box p\).
-
Consider the rule of inference: \(\Box \varphi / \varphi\) Justify the claims below:
The rule above preserves validity with respect to the class of all frames.
We target the contrapositive.
If \(\varphi\) is not valid in all frames, then neither is \(\Box \varphi\) valid in all frames.
Suppose \((W, R, V)\) is a model based on a frame \((W,R)\) such that for some \(w \in W\), \((W, R, V), w \nVdash \varphi\). Fix such a world \(w\in W\). We may now specify a model \((W^\ast, R^\ast, V^\ast)\) such that for some \(w^\ast \in W^\ast\), \((W^\ast, R^\ast, V^\ast) \nVdash \Box \varphi\). Define:
\(W^\ast = W \cup \{@\}\), where \(@ \notin W\).
\[R^\ast = R \cup \{(@, w)\}\]\(V^\ast (p) = V(p)\) for all propositional variable \(p\).
Since \(@\) has access to \(w\) but to no other world at \(W^\ast\) and \((W^\ast, R^\ast, V^\ast), w \nVdash \varphi\), we have \((W^\ast, R^\ast, V^\ast), @ \nVdash \Box \varphi\). It follows that \((W^\ast, R^\ast, V^\ast), @ \nVdash \Box \varphi\).