problems

axiomatic derivations 

1. Justify the facts given below:

   1. \(\Box \varphi/\varphi\) is a derived rule of inference for \(\textsf{K}\).

   2. \(\Box \varphi/\varphi\) is a derived rule of inference for \(\textsf{KD}\).

   3. \(\Box \varphi/\varphi\) is a derived rule of inference for \(\textsf{KT}\).

   Consider a transformation \(\sigma\) from formulas of \(\mathcal{L}^{\Box}\) into formulas of \(\mathcal{L}^{\Box}\) defined by the recursion:
   

   \(\begin{array}{lll} \sigma(p) & = & p\\ \sigma(\neg \varphi) & = &\neg \sigma(\varphi)\\ \sigma(\varphi \to \psi) & = & \sigma(\varphi) \to \sigma(\varphi)\\ \sigma (\Box \varphi) & = & \varphi\\ \end{array}\)
   

   In other words, \(\sigma\) scans a formula for subformulas of the form \(\Box \psi\) and deletes the first occurrence of a modal operator in those formulas. Thus for example \(\sigma(\Box p \to \Box \Box p)\) is just the formula: \(p \to \Box p\), and \(\sigma(\Box p \to \Diamond p)\), which is \(\sigma(\Box p \to \neg \Box \neg p)\) becomes the formula: \(p \to \neg \neg p\).

   For the first two systems \(\Sigma\) mentioned above, use an induction on the length of proofs in \(\Sigma\) to prove:

   \[\begin{array}{llll} \text{if} & \vdash_{\Sigma} \varphi, & \text{then} & \vdash_{\Sigma} \sigma(\varphi)\\ \end{array}\]

   The rule of inference we want is a special case of this more general result.

   
   

   Consider the case of \(\textsf{K}\). We will proceed by complete induction without a base case on the length of proofs in \(\textsf{K}\). We argue that if for each \(m < n\), if there is a proof of \(\varphi\) in \(\textsf{K}\) of length less or equal to \(m\) only if there is a proof of \(\sigma(\varphi)\) in \(\textsf{K}\), then if there is a proof of of \(\varphi\) in \(\textsf{K}\) of length less or equal to \(n\) only if there is a proof of \(\sigma(\varphi)\) in \(\textsf{K}\).

   Suppose that for each \(m < n\), there is a proof of \(\varphi\) in \(\textsf{K}\) of length less or equal to \(m\) only if there is a proof of \(\sigma(\varphi)\) in \(\textsf{K}\). Now, let \(\langle \chi_1, \dots, \chi_n \rangle\) be a proof of \(\varphi\) in \(\textsf{K}\) of length \(n\). That means that \(\chi_n = \varphi\) and for all \(i \leq n\), \(\chi_i\) is either (a) a tautology, or (b) an axiom of \(\textsf{K}\), or (b) an outcome of an application of necessitation to a prior line, or (d) an outcome of an application of modus ponens to two prior lines.

   1. If \(\varphi\) is a tautology, then \(\sigma(\varphi)\) is a tautology. Strictly speaking, we would have to use a separate induction to convince ourselves that if \(\varphi\) is derivable from \(\psi_1, \cdots, \psi_n\) in propositional logic, then \(\sigma(\varphi)\) is itself derivable from \(\sigma(\psi_1), \cdots , \sigma(\psi_n)\) in propositional logic.

   2. \(\varphi\) is an axiom of \(\textsf{K}\) of the form \(\Box (\psi \to \chi) \to (\Box \psi \to \Box \chi)\).

      Note that \(\sigma(\varphi)\) becomes \((\psi \to \chi) \to (\psi \to \chi)\), which is a theorem of \(\textsf{K}\).

   3. \(\varphi\) is the necessitation of \(\chi_m\), \(\Box \chi_m\), for some \(m < n\)

      That means there is a proof of \(\chi_m\) in \(\textsf{K}\) of length \(m < n\). But notice that \(\sigma(\varphi)\) is just \(\chi_m\), and \(\vdash_{\textsf{K}} \sigma(\varphi)\).

   4. \(\varphi\) is the consequent of a conditional \((\psi \to \varphi)\), which is \(\chi_i\) for some \(i < n\) and \(\psi\) is \(\chi_j\) for some \(j<n\). That means that there are proofs of each \((\psi \to \varphi)\) and \(\psi\) in \(\textsf{K}\) of length less than \(n\). By inductive hypothesis, \(\vdash_{\textsf{K}} \sigma(\psi \to \varphi)\) and \(\vdash_{\textsf{K}} \sigma(\psi)\). Since \(\sigma(\psi \to \varphi)\) is \(\sigma(\psi) \to \sigma(\varphi)\), \(\vdash_{\textsf{K}} \sigma(\psi) \to \sigma(\varphi)\), whence \(\vdash_{\textsf{K}} \sigma(\varphi)\).

   For \(\textsf{KD}\), we simply expand 2 to include the case in which \(\varphi\) is an instance of \(\textsf{D}\) of the form \(\Box \varphi \to \Diamond \varphi\), which is just \(\Box \varphi \to \neg \Box \neg \varphi\). Then:
   

   \(\begin{array}{lll} \sigma(\Box \varphi \to \neg \Box \neg \varphi) & = & \sigma(\varphi) \to \sigma(\neg \Box \neg \varphi) \\ & = & \varphi \to \neg \sigma(\Box \neg \varphi) \\ & = & \varphi \to \neg \neg \varphi \end{array}\)
   

   Since \(\varphi \to \neg \neg \varphi\) is a tautology, it is a theorem of \(\textsf{KD}\).

   We are not able to use the same strategy for \(\textsf{KT}\) because there is no guarantee that the transformation of \(\Box \varphi \to \varphi\) is a tautology, for example, \(\sigma(\Box (\Box p \to \Box q) \to (\Box p \to \Box q))\) is just \((\Box p \to \Box q) \to (p \to q)\), which is not a tautology. Instead, we may simply explain how to expand a proof of \(\Box \varphi\) into a proof of \(\varphi\) by appeal to axiom \(\textsf{T}\):
   

   \(\begin{array}{llll} 1 & \cdots & \\ 2 & \cdots & \\ n & \Box \varphi & \\ n+1 & \Box \varphi \to \varphi & \textsf{T}[\varphi/p]\\ n+2 & \varphi & \textsf{MP} 1, 2\\ \end{array}\)
   

   
   

2. Prove \(\textsf{KB4}\) is a proper extension of \(\textsf{K5}\). That is,

   1. All theorems of \(\textsf{K5}\) are theorems of \(\textsf{KB4}\).

      Here is a proof schema for substitution instances of axiom \(\textbf{5}\): \(\begin{array}{llll} 1 & \Diamond \varphi \to \Box \Diamond \Diamond \varphi & \textsf{B}[\Diamond \varphi/p]\\ 2 & \Diamond \Diamond \varphi \to \Diamond \varphi & \textsf{4}_\Diamond [\varphi/p]\\ 3 & \Box \Diamond \Diamond \varphi \to \Box \Diamond \varphi & \textsf{RK} 2\\ 4 & \Diamond \varphi \to \Box \Diamond \varphi & \textsf{PL} 1, 3\\ \end{array}\)

   2. Not all theorems of \(\textsf{KB4}\) are theorems of \(\textsf{K5}\).

      \(\textsf{K5}\) is sound with respect to the class of euclidean frames, which means that all theorems of \(\textsf{K5}\) are valid in all euclidean frames. On the other hand, not all substitution instances of axiom \(\textsf{B}\) or \(\textsf{4}\) are valid in all euclidean frames. Here is a model based on a euclidean frame in which \(p \to \Box \Diamond p\) fails:

      

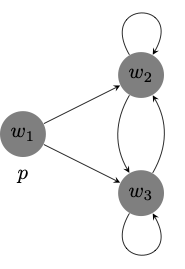
      Here is similarly a model based on a euclidean frame in which \(\Box p \to \Box \Box p\) fails:

      

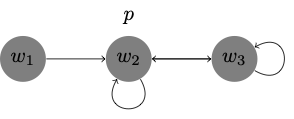
3. Prove that \(\textsf{K5}\) proves the necessitation of every axiom of \(\textsf{KB4}\). That is:

   1. \(\vdash_{\textsf{K5}} \Box (\varphi \to \Box \Diamond \varphi)\)
      

      Here is a proof schema for necessitations of axiom \(\textsf{B}\):

      \(\begin{array}{llll} 1 & \Box \Diamond \varphi \to (\varphi \to \Box \Diamond \varphi) & \textsf{PL}\\ 2 & \Diamond \varphi \to \Box \Diamond \varphi & \textsf{5}\\ 3 & \Diamond \varphi \to (\varphi \to \Box \Diamond \varphi) & \textsf{PL} \ 1, 2\\ 4 & \Box \Diamond \varphi \to \Box(\varphi \to \Box \Diamond \varphi) & \textsf{RK} \ 3 \\ 5 & \Diamond \varphi \to \Box(\varphi \to \Box \Diamond \varphi) & \textsf{PL} \ 2, 4 \\ 6 & \neg \varphi \to (\varphi \to \Box \Diamond \varphi) & \textsf{PL} \\ 7 & \Box \neg \varphi \to \Box (\varphi \to \Box \Diamond \varphi) & \textsf{RK} \ 6\\ 8 & \neg \Diamond \varphi \to \Box \neg \varphi & \textsf{Def} \ \Diamond, \textsf{PL}\\ 9 & \neg \Diamond \varphi \to \Box (\varphi \to \Box \Diamond \varphi) & \textsf{PL} \ 7, 8\\ 10 & \Box (\varphi \to \Box \Diamond \varphi) & \textsf{PL} \ 5, 9 \end{array}\)
      

      
      

      There is an alternative justification, which appeals to the completeness of \(\textsf{K5}\) with respect to the class of euclidean frames. Since every substitution instance of the formula \(\Box (p \to \Box \Diamond p)\) is valid in all euclidean frames, by completeness, they should be provable in \(\textsf{K5}\).

      For let a world \(w\) be a member of \(W\) in an euclidean frame \(( W, R)\). We set out to show that \((W, R, V), w \Vdash \Box (\varphi \to \Box \Diamond \varphi)\) no matter what \(V\) may be. That is, for each \(u\in W\), if \(Rwu\), then \((W, R, V), u \Vdash \varphi \to \Box \Diamond \varphi\). Notice that if \(Rwu\), since \(R\) is euclidean on \(W\), \(Ruu\). Now, suppose \((W, R, V), u \Vdash \varphi\) and let $v\in W$ be such that \(Ruv\). Since \(R\) is euclidean on \(W\), we infer that \(Rvu\), which means that \((W, R, V), v \Vdash \Diamond \varphi\). Generalizing, we have \((W, R, V), u \Vdash \Box \Diamond \varphi\) and thus \((W, R, V), u \Vdash \varphi \to \Box \Diamond \varphi\).

   2. \(\vdash_{\textsf{K5}} \Box (\Box \varphi \to \Box \Box \varphi)\)
      

      Here is a proof schema for necessitations of axiom \(\textsf{4}\):

      \(\begin{array}{llll} 1 & \Diamond \Box \varphi \to \Box \varphi & \textsf{5}_\Diamond \\ 2 & \Box \Diamond \Box \varphi \to \Box \Box \varphi & \textsf{RK} \ 1 \\ 3 & \Box (\Box \varphi \to \Box \Diamond \Box \varphi) & \Box \textsf{B}[\Box \varphi/p]\\ 4 & (\Box \varphi \to \Box \Diamond \Box \varphi) \to ((\Box \Diamond \Box \varphi \to \Box \Box \varphi) & \textsf{PL}\\ & \to (\Box \varphi \to \Box \Box \varphi)) & \\ 5 & \Box (\Box \varphi \to \Box \Diamond \Box \varphi) \to \Box ((\Box \Diamond \Box \varphi \to \Box \Box \varphi) & \textsf{RK} \ 4\\ & \to (\Box \varphi \to \Box \Box \varphi)) & \\ 6 & \Box (\Box \Diamond \Box \varphi \to \Box \Box \varphi) & \textsf{RN} \ 2\\ 7 & \Box (\Box \varphi \to \Box \Box \varphi) & \textsf{PL} \ 5, 6 \end{array}\)
      

      There is an alternative justification, which appeals to the completeness of \(\textsf{K5}\) with respect to the class of euclidean frames. Since every substitution instance of the formula \(\Box (\Box p \to \Box \Box p)\) is valid in all euclidean frames, by completeness, they should be provable in \(\textsf{K5}\).

      For let a world \(w\) be a member of \(W\) in an euclidean frame \(( W, R)\). We set out to show that \((W, R, V), w \Vdash \Box (\Box \varphi \to \Box \Box \varphi)\) no matter what \(V\) may be. That is, for each \(u\in W\), if \(Rwu\), then \((W, R, V), u \Vdash \Box \varphi \to \Box \Box \varphi\). Notice that if \(Rwu\), since \(R\) is euclidean on \(W\), \(Ruu\). Now, suppose \((W, R, V), u \Vdash \Box \varphi\) and let $v\in W$ be such that \(Ruv\). We argue that \((W, R, V), v \Vdash \Box \varphi\). To that purpose let \(t \in W\) be such that \(Rvt\). Since \(R\) is euclidean on \(W\) and we have \(Ruv\) and \(Ruu\), we know that \(Rvu\). Furthermore, since \(Rvu\) and \(Rvt\), we have that \(Rut\). But since \(\Box \varphi\) is true at \(u\), \(\varphi\) is true at \(t\). Generalizing, we have \((W, R, V), v \Vdash \Box \varphi\) and \((W, R, V), u \Vdash \Box \varphi \to \Box \Box \varphi\).

   
   

4. Justify the facts given below:

   1. \(\Box \varphi / \varphi\) is not a derived rule of inference for \(\textsf{K5}\).

      This is an immediate consequence of problems 2 and 3. On the one hand, by 3a, every necessitation of every instance of \(\textsf{B}\) is provable in \(\textsf{K5}\). On the other hand, by 2b, not every instance of \(\textsf{B}\) are provable in \(\textsf{K5}\).

   2. \(\Box \varphi/\varphi\) is not a derived rule of inference for \(\textsf{KB4}\)

      Notice, first, that \(\vdash_{\textsf{KB4}} \Box(\Box \varphi \to \varphi)\).

      \(\begin{array}{llll} 1 & \Diamond \Box \varphi \to \Box \varphi & \textsf{5}_\Diamond \\ 2 & \neg \Box \neg \Box \varphi \to \Box \varphi & \textsf{Def} \Diamond \ 1\\ 3 & \Box \neg \Box \varphi \vee \Box \varphi & \textsf{PL} \ 2 \\ 4 & (\Box \neg \Box \varphi \vee \Box \varphi) \to \Box (\neg \Box \varphi \vee \varphi) & \textsf{K} \\ 5 & \Box (\neg \Box \varphi \vee \varphi) & \textsf{MP} \ 3, 4 \\ 6 & \Box (\Box \varphi \to \varphi) & \textsf{PL} \ 5 \\ \end{array}\)
      

      On the other hand, \(\nvdash_{\textsf{KB4}} \Box \varphi \to \varphi\). For \(\textsf{KB4}\) is sound with respect to the class of symmetric and transitive frames, and not all symmetric and transitive frames are reflexive. There are, in other words, models based on symmetric and transitive frames in which \(\Box \varphi \to \varphi\) fails.

      \(\Box \varphi/\varphi\) is not even a derived rule of inference for \(\textsf{KB}\).

      Notice, first, that \(\vdash_{\textsf{KB}} \Box \Diamond \top\). \(\begin{array}{llll} 1 & \top \to \Box \Diamond \top & \textsf{B} \\ 2 & \top & PL \\ 3 & \Box \Diamond\top & \textsf{PL} \ 1, 2 \\ \end{array}\) On the other hand, \(\not \vdash_{\textsf{KB}} \Diamond \top\). For \(\textsf{KB}\) is sound with respect to the class of symmetric frames, and not all symmetric frames are serial. Consider a frame consisting of a dead end \(w\) from which nothing is accessible. That would be a frame validating \(\Box \Diamond \top\) without validating \(\Diamond \top\).