gabriel uzquiano

problems

deontic logic

$\textsf{KDU}$ is a deontic logic that extends $\textsf{KD}$ with all substitution instances of the axiom:

$\textsf{O}(\textsf{O}p \to p) \tag{U}$
Justify the facts given below:

$\textsf{KDU}$ is sound and complete with respect to the class of serial and weakly reflexive frames. You may take for granted that (i) if $\textsf{KDU}$-consistent, a formula $\varphi$ is true at some world of the canonical model for $\textsf{KDU}$ and that (ii) the canonical model for $\textsf{KDU}$ is serial, which is a consequence of Proposition 8.2 in section 8.2.

We must verify that the canonical model for $\textsf{KDU}$ is weakly reflexive.

Let $\Gamma, \Delta \in W_{\textsf{KDU}}$ be such that $R_{\textsf{KDU}}\Gamma \Delta$. We should now verify that $R_{\textsf{KDU}} \Delta \Delta$. That is, for each formula $\varphi$, we check that $\Box \varphi \in \Delta$ only if $\varphi \in \Delta$. Now, let $\varphi$ be such that $\Box \varphi \in \Delta$. Since $\vdash_{\textsf{KDU}} \Box (\Box \varphi \to \varphi)$, we know that $\Box (\Box \varphi \to \varphi) \in \Gamma$. Since $R_{\textsf{KDU}}\Gamma \Delta$, we infer $\Box \varphi \to \varphi \in \Delta$. So, since $\Delta$ is closed under $\textsf{MP}$, we conclude that $\varphi \in \Delta$.
$\textsf{KDU}$ is not closed under the derived rule of inference $\textsf{P}\varphi/\varphi$.

Axioms $\textsf{U}$ and $\textsf{D}$ make sure that $\vdash_{\textsf{KDU}} \textsf{P}(\textsf{O}p \to p)$. But we now argue that $\nvdash_{\textsf{KDU}} \textsf{O}p \to p$. Since $\textsf{KDU}$ is complete with respect to the class of serial and weakly reflexive frames, it suffices to note that $\textsf{O}p \to p$ is not valid in some serial and weakly reflexive frames. Consider, for example, the serial and weakly reflexive model depicted below, and notice that $\textsf{O}p \to p$ fails at $w_1$.
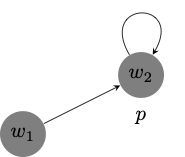
$\textsf{KD}$ is closed under the derived rule of inference $\textsf{P}\varphi/\varphi$.

This is a simple corollary of problem 1.2 in problem set 5.
$\textsf{KDU}$ proves every substitution instance of $\textsf{P}p \to \textsf{PP}p$.

Here is a derivation schema:

$\begin{array}{llll} 1 & \textsf{O}(\textsf{O}\varphi \to \varphi) & U[\varphi/p] \\ 2 & \textsf{O}(\textsf{O}\varphi \to \varphi) \to (\textsf{O}\textsf{O}\varphi \to \textsf{O}\varphi) & \textsf{K}[\textsf{O}\varphi/p, \varphi/q] \\ 3 & \textsf{O}\textsf{O}\varphi \to \textsf{O}\varphi & \textsf{PL} \ 1, 2 \end{array}$

But the formula $\textsf{O}\textsf{O}\varphi \to \textsf{O}\varphi$ is just the dual of $\textsf{P}\varphi \to \textsf{PP}\varphi$ to which is equivalent modulo $\textsf{K}$.

We may reason semantically as well. The formula $\textsf{P}p \to \textsf{PP}p$ defines the class of dense frames, but every serial and weakly reflexive model is dense. The definability claim is briefly mentioned in problem set 6.
$\textsf{KDU}$ proves every substitution instance of $\textsf{O}p \to \textsf{O}\textsf{P}p$.

Here is a derivation schema:

$\begin{array}{llll} 1 & (\textsf{O}\neg \varphi \to \neg \varphi) \to (\varphi \to \textsf{P}\varphi) & \textsf{PL}\\ 2 & \textsf{O}(\textsf{O}\neg \varphi \to \neg \varphi) \to \textsf{O}(\varphi \to \textsf{P}\varphi) & \textsf{RN} 1\\ 3 & \textsf{O}(\textsf{O}\neg \varphi \to \neg \varphi) & \textsf{U}[\neg \varphi/p]\\ 4 & \textsf{O}(\varphi \to \textsf{P}\varphi) & \textsf{PL} \ 2, 3\\ 5 & \textsf{O}(\varphi \to \textsf{P}\varphi) \to (\textsf{O}\varphi \to \textsf{O}\textsf{P}\varphi) & \textsf{K}[\varphi/p, \textsf{P}\varphi/q]\\ 6 & \textsf{O}p \to \textsf{O}\textsf{P}p) & \textsf{PL} \ 4, 5 \end{array}$
$\textsf{KD5}$ is a proper extension of $\textsf{KDU}$

This is a corollary of the fact that $\vdash_{K5} \textsf{O} (\textsf{O}\varphi \to \varphi)$. For a proof, you may consult the solution to 4.2 in problem set 5. Alternatively, you can reason semantically and notice that every euclidean frame is weakly reflexive.

On the other hand, some serial and weakly reflexive models are not euclidean. All such models will falsify $\textsf{P}p \to \textsf{O}\textsf{P}p$, which is just axiom $\textsf{5}$. Since $\textsf{KDU}$ is, by problem 1 above, sound and complete with respect to serial and reflexive models, we conclude that $\nvdash_{\textsf{KDU}} \textsf{P}p \to \textsf{O}\textsf{P}p$.
Neither $\textsf{KD4}$ nor $\textsf{KDU}$ are extensions of each other.

We reason semantically.

$\textsf{KD4}$ is not an extension of $\textsf{KDU}$ because $\textsf{4}$ is not valid in every serial and weakly reflexive frame. Consider, for example, the serial and weakly reflexive model depicted below, and notice that $\textsf{O}p \to \textsf{O}\textsf{O}p$ fails at $w_1$.

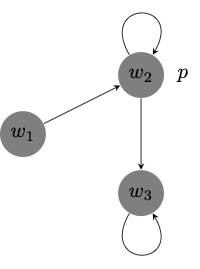
$\textsf{KDU}$ is not an extension of $\textsf{KD4}$ because $\textsf{U}$ is not valid in every serial and transitive frame. Consider, for example, the serial and transitive model depicted below, and notice that $\textsf{O}(\textsf{O}p \to p)$ fails at $w_1$.

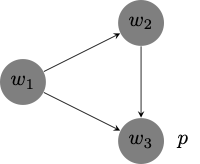
This is because $\textsf{O}p \to p$ fails at $w_2$, which is accessible from $w_1$.