7 Axiomatic Derivations
We now aim for an alternative characterization of the set of formulas of \(\mathcal{L}^\Box\) that are valid in different classes of frames. We will begin with a system K, whose theorems are all and only formulas of \(\mathcal{L}^\Box\) that are valid in every frame. We will later consider extensions of that system, whose theorems are all and only formulas valid in every frame in a certain class, e.g., reflexive, symmetric, transitive, etc.
7.1 The Minimal Normal Modal Logic
The minimal normal modal logic consists of an infinite set of axioms and two rules of inference.
The axioms of \(\textsf{K}\) include:
substitution instances of tautologies of propositional logic
substitution instances of the axiom: \[\tag{$\textsf{K}$} \Box(p \to q) \to (\Box p \to \Box q)\\ \]
The rules of inference of \(\textsf{K}\) include:
- Modus Ponens:
\[\tag{$\textsf{MP}$} \varphi, (\varphi \to \psi)/\psi %\text{If} \ \vdash \varphi \ \text{and} \ \vdash (\varphi \to \psi), \ \text{then} \ \vdash \psi \]
- Necessitation:
\[\tag{$\textsf{N}$} \varphi/\Box \varphi %\text{If} \ \vdash \varphi \ \text{then} \ \vdash \Box \varphi \]
A derivation in \(\textsf{K}\) is, as usual, a finite sequence of formulas \((\chi_1, \dots, \chi_n)\) of \(\mathcal{L}^\Box\), each of them
a substitution instance of \(\textsf{K}\)
an outcome of an application of \(\textsf{MP}\) to two prior formulas
an outcome of an application of \(\textsf{N}\) to a prior formula
A formula \(\varphi\) of \(\mathcal{L}^\Box\) is a theorem of \(\textsf{K}\), written \(\vdash_{\textsf{K}} \varphi\), if, and only if, some proof in K ends with the formula \(\varphi\).
The axioms of the minimal modal logic \(\textsf{K}\) are valid in all frames, and the rules of inference preserve validity in all frames. So, every theorem of \(\textsf{K}\) is valid in every frame.
Theorem 7.1 All substitution instances of axiom \(\textsf{K}\) is valid in all frames. \[\tag{$\textsf{K}$} \Box(p \to q) \to (\Box p \to \Box q)\\ \]
Proof. Consider a substitution instance of axiom \(\textsf{K}\): \[ \Box (\varphi \to \psi) \to (\Box \varphi \to \Box \psi). \]
Let \((W, R)\) be a frame and let \((W, R, V)\) be a model based on that frame. We argue that \((W,R,V) \models \Box (\varphi \to \psi) \to (\Box \varphi \to \Box \psi)\). To that end, let \(w \in W\) and suppose that \((W,R,V), w \Vdash \Box (\varphi \to \psi)\) and \((W,R,V), w \Vdash \Box \varphi\). If \(u\in W\) is such that \(Rwu\), then \((W,R,V), u \Vdash \varphi \to \psi\) and \((W,R,V) \Vdash \varphi\). Therefore, \((W,R,V), u \Vdash \psi\). Generalizing, we find \((W,R,V), w \Vdash \Box \psi\).
\(\blacksquare\)
While it is a purely mechanical procedure to check whether a finite sequence of formulas is a proof in a given system, it may take some skill and experience to find one. There is no perfectly general recipe for this, but as a general piece of advice, it helps to spend some time considering the question of why the formula should be valid. Since proofs and theorems of \(\textsf{K}\) track validity in all frames, the question of validity may on occasion guide us to a proof.
7.1.1 Derived Rules of Inference
One important observation at this point is that we are entitled to propositional inferences within the system. If two formulas are propositionally equivalent, then you should feel free to move from one to the other. Here is a formal justification of that fact.
Theorem 7.2 If \(\vdash_{\textsf{K}} \varphi_1, \dots, \vdash_{\textsf{K}} \varphi_n\) and \(\psi\) is derivable from \(\{\varphi_1, \dots, \varphi\}\) in propositional logic, then \(\vdash_{\textsf{K}} \psi\).
Proof. Given the Deduction Theorem for Propositional Logic, if \(\psi\) is derivable from \(\{\varphi_1, \dots, \varphi\}\) in propositional logic, then \(\varphi_1 \to (\varphi_2 \to (\dots (\varphi_n \to \psi)\dots))\) is a theorem of propositional logic and thus a theorem of \(K\). By repeated applications of Modus Ponens, we infer \(\vdash_\textsf{K} \psi\).
\(\blacksquare\)
We are similarly able to justify derived rules of inference, which will help us take a more direct route between two steps in a proof.
Theorem 7.3 If \(\vdash_{\textsf{K}} \varphi \to \psi\), then \(\vdash_{\textsf{K}} \Box \varphi \to \Box \psi\).
Proof. We may transform a derivation of \(\varphi \to \psi\) into a derivation of \(\varphi \to \Box \psi\). \[ \begin{array}{lllll} 1 & & \varphi \to \psi & \\ 2 & & \Box (\varphi \to \psi) & \textsf{RN} \ 1\\ 3 & & \Box (\varphi \to \psi) \to (\Box \varphi \to \Box \psi) & \textsf{K}[\varphi/p, \psi/q]\\ 4 & & \Box \varphi \to \Box \psi & \textsf{MP} \ 2, 3\\ \end{array} \]
\(\blacksquare\)
This justifies a derived rule of inference:
\[\tag{$\textsf{RK}$} \text{If} \ \vdash \varphi \to \psi \ \text{then} \ \vdash \Box \varphi \to \Box \psi \]
\[\tag{$\textsf{RK}\Diamond$} \text{If} \ \vdash \varphi \to \psi \ \text{then} \ \vdash \Diamond \varphi \to \Diamond \psi \]
Theorem 7.4 If \(\vdash_\textsf{K} \varphi \to \psi\), then \(\vdash_\textsf{K} \Diamond \varphi \to \Diamond \psi\).
Proof. We may transform a proof of \(\varphi \to \psi\) into a proof of \(\Diamond \varphi \to \Diamond \psi\) \[ \begin{array}{lllll} 1 & & \varphi \to \psi & \\ 2 & & \neg \psi \to \neg \varphi & \textsf{PL} \ 1 \\ 3 & & \Box \neg \psi \to \Box \neg \varphi & \textsf{RK} \ 2 \\ 4 & & \neg \Box \neg \varphi \to \neg \Box \neg \psi & \textsf{PL} \ 3\\ 7 & & \Diamond \varphi \to \Diamond \psi & \textsf{Def} \ \Diamond \ 4\\ \end{array} \]
\(\blacksquare\)
More generally, if \(Q\) is a string of modal operators, we are in a position to justify the derived rule of inference:
\[\tag{$\textsf{RK}Q$} \text{If} \ \vdash_K \varphi \to \psi \ \text{then} \ \vdash Q \varphi \to Q \psi \]
Consider the derived rule of inference:
\[\tag{$\textsf{RK}\Box \Diamond$} \text{If} \ \vdash \varphi \to \psi \ \text{then} \ \vdash \Box \Diamond \varphi \to \Box \Diamond \psi \] Here is how to transform a derivation of \(\varphi \to \psi\) into a derivation of \(\Box \Diamond \varphi \to \Box \Diamond \psi\):
\[ \begin{array}{lllll} 1 & & \varphi \to \psi & \\ 2 & & \Diamond \varphi \to \Diamond \psi & \textsf{RK}\Diamond \ 1\\ 3 & & \Box \Diamond \varphi \to \Box \Diamond \psi & \textsf{RK} \ 2\\ \end{array} \]
7.1.2 Theorems of \(\textsf{K}\)
We now exploit some of these derived rules of inference to prove some theorems of the minimal normal modal logic \(\textsf{K}\).
Proposition 7.1 \(\vdash_\textsf{K} \Box (\varphi \to \psi) \to (\Diamond \varphi \to \Diamond \psi)\)
\[ \begin{array}{lllll} 1 & & (\varphi \to \psi) \to (\neg \psi \to \neg \varphi) & \textsf{PL} \\ 2 & & \Box (\varphi \to \psi) \to \Box(\neg \psi \to \neg \varphi) & \textsf{RK} \ 1 \\ 3 & & \Box (\neg \psi \to \neg \varphi) \to (\Box \neg \psi \to \Box \neg \varphi) & \textsf{K}[\neg \psi/p, \neg \varphi/q] \\ 4 & & (\Box \neg \psi \to \Box \neg \varphi) \to (\neg \Box \neg \varphi \to \neg \Box \neg \psi) & \textsf{PL}\\ 5 & & \Box (\varphi \to \psi) \to (\neg \Box \neg \varphi \to \neg \Box \neg \psi) & \textsf{PL} \ 2, 3, 4\\ 6 & & \Box (\varphi \to \psi) \to (\Diamond \varphi \to \Diamond \psi) & \textsf{Def} \ \Diamond \ 6\\ \end{array} \]
Given those observations, it is simple to justify:
Proposition 7.2 \(\vdash_\textsf{K} \Diamond p \wedge \Box (p \to q) \to \Diamond q\)
For \(\Diamond p \wedge \Box (p \to q) \to \Diamond q\) is propositionally equivalent to \(\Box (p \to q) \to (\Diamond p \to \Diamond q)\).
Other well-known theorems of the minimal logic K are principles such as the distribution of \(\Box\) over \(\wedge\) and the distribution of \(\Diamond\) over \(\vee\).
Proposition 7.3 \(\vdash_\textsf{K} \Box(\varphi \wedge \psi) \to (\Box \varphi \wedge \Box \psi)\)
\[ \begin{array}{lllll} 1 & & (\varphi \wedge \psi) \to \varphi & \textsf{PL} \\ 2 & & \Box (\varphi \wedge \psi) \to \Box \varphi & \textsf{RK} \ 1 \\ 3 & & (\varphi \wedge \psi) \to \psi & \textsf{PL} \\ 4 & & \Box (\varphi \wedge \psi) \to \Box \psi & \textsf{RK} \ 3 \\ 5 & & \Box (\varphi \wedge \psi) \to (\Box \varphi \wedge \Box \psi) & \textsf{PL} \ 2, 4\\ \end{array} \]
Proposition 7.4 \(\vdash_\textsf{K} (\Box \varphi \wedge \Box \psi) \to \Box (\varphi \wedge \psi)\)
This proof combines the use of a distribution rule with an instance of K. \[ \begin{array}{lllll} 1 & & \varphi \to (\psi \to (\varphi \wedge \psi)) & \textsf{PL} \\ 2 & & \Box \varphi \to \Box (\psi \to (\varphi \wedge \psi)) & \textsf{RK} \ 1\\ 3 & & \Box (\psi \to (\varphi \wedge \psi)) \to (\Box \psi \to \Box (\varphi \wedge \psi)) & \textsf{K}[\psi/p, (\varphi \wedge \psi)/q]\\ 4 & & \Box \varphi \to (\Box \psi \to \Box (\varphi \wedge \psi)) & \textsf{PL} \ 2, 3\\ 5 & & (\Box \varphi \wedge \Box \psi) \to \Box (\varphi \wedge \psi) & \textsf{PL} \ 4\\ \end{array} \]
Proposition 7.5 \(\vdash_\textsf{K} (\Diamond \varphi \vee \Diamond \psi) \to \Diamond (\varphi \vee \psi)\)
The strategy behind the proof is to exploit the fact that \(\Diamond\) is a dual of \(\Box\), that is, \(\Diamond\) is \(\neg \Box \neg\), and the fact that the negation of a disjunction is propositionally equivalent to a conjunction of negations. When we combine them with the fact that \(\Box\) distributes over \(\wedge\), we have a proof ot the principle.
\[ \begin{array}{lllll} 1 & & \neg \Diamond (\varphi \vee \psi) \to \neg \neg \Box \neg (\varphi \vee \psi) & \textsf{Def} \ \Diamond\\ 2 & & \neg \Diamond (\varphi \vee \psi) \to \Box \neg (\varphi \vee \psi) & \textsf{PL} \ 1\\ 3 & & \neg (\varphi \vee \psi) \to (\neg \varphi \wedge \neg \psi) & \textsf{PL}\\ 4 & & \Box \neg (\varphi \vee \psi) \to \Box (\neg \varphi \wedge \neg \psi) & \textsf{RK} \ 3\\ 5 & & \Box (\neg \varphi \wedge \neg \psi) \to (\Box \neg \varphi \wedge \Box \neg \psi) & \textsf{Prop} \ 7.5\\ 6 & & (\Box \neg \varphi \wedge \Box \neg \psi) \to \neg (\neg \Box \neg \varphi \vee \neg \Box \neg \psi) & \textsf{PL} \\ 7 & & \neg (\neg \Box \neg \varphi \vee \neg \Box \neg \psi) \to \neg (\Diamond \varphi \vee \Diamond \psi) & \textsf{Def} \ \Diamond\\ 8 & & \Box \neg (\varphi \vee \psi) \to \neg (\Diamond \varphi \vee \Diamond \psi) & \textsf{PL} \ 5, 6, 7\\ 9 & & \neg \Diamond (\varphi \vee \psi) \to \neg (\Diamond \varphi \vee \Diamond \psi) & \textsf{PL} \ 2, 8\\ 10 & & (\Diamond \varphi \vee \Diamond \psi) \to \Diamond (\varphi \vee \psi) & \textsf{PL} \ 9\\ \end{array} \]
Proposition 7.6 \(\vdash_\textsf{K} \Diamond (\varphi \vee \psi) \to (\Diamond \varphi \vee \Diamond \psi)\)
This time we exploit the fact that a conjunction of necessitations entails the necessitation of a conjunction. \[ \begin{array}{lllll} 1 & & \neg (\Diamond \varphi \vee \Diamond \psi) \to \neg (\neg \Box \neg \varphi \vee \neg \Box \neg \psi) & \textsf{Def} \ \Diamond \\ 2 & & \neg (\neg \Box \neg \varphi \vee \neg \Box \neg \psi) \to (\Box \neg \varphi \wedge \Box \neg \psi) & \textsf{PL} \\ 3 & & (\Box \neg \varphi \wedge \Box \psi) \to \Box (\neg \varphi \wedge \neg \psi) & \textsf{Prop} \ 7.6\\ 4 & & \neg (\Diamond \varphi \vee \Diamond \psi) \to \Box (\neg \varphi \wedge \neg \psi) & \textsf{PL} \ 1, 2, 3\\ 5 & & (\neg \varphi \wedge \neg \psi) \to \neg (\varphi \vee \psi) & \textsf{PL} \\ 6 & & \Box (\neg \varphi \wedge \neg \psi) \to \Box \neg (\varphi \vee \psi) & \textsf{RK} \ 5 \\ 7 & & \neg (\Diamond \varphi \vee \Diamond \psi) \to \Box \neg (\varphi \vee \psi) & \textsf{PL} \ 4, 6\\ 8 & & \Box \neg (\varphi \vee \psi) \to \neg \neg \Box \neg (\varphi \vee \psi) & \textsf{PL} \\ 9 & & \neg \neg \Box \neg (\varphi \vee \psi) \to \neg \Diamond (\varphi \vee \psi) & \textsf{Def} \ \Diamond\\ 10 & & \neg (\Diamond \varphi \vee \Diamond \psi) \to \neg \Diamond (\varphi \vee \psi) & \textsf{PL} \ 7, 8, 9\\ 11 & & \Diamond (\varphi \vee \psi) \to (\Diamond \varphi \vee \Diamond \psi) & \textsf{PL} \ 10 \end{array} \]
We conclude with another helpful theorem of \(\textsf{K}\).
Proposition 7.7 \(\vdash_\textsf{K} (\Diamond \varphi \wedge \Box \psi) \to \Diamond (\varphi \wedge \psi)\)
\[ \begin{array}{lllll} 1 & & \neg (\varphi \wedge \psi) \to (\psi \to \neg \varphi) & \textsf{PL} \\ 2 & & \Box \neg (\varphi \wedge \psi) \to \Box (\psi \to \neg \varphi) & \textsf{RK} \ 1 \\ 3 & & \Box (\psi \to \neg \varphi) \to (\Box \psi \to \Box \neg \varphi) & \textsf{K}[\psi/p, \neg \varphi/q] \\ 4 & & \Box \neg (\varphi \wedge \psi) \to (\Box \psi \to \Box \neg \varphi) & \textsf{PL} \ 2, 3\\ 5 & & \neg (\Box \psi \to \Box \neg \varphi) \to \neg \Box \neg (\varphi \wedge \psi) & \textsf{PL} \ 4 \\ 6 & & \neg (\Box \psi \to \Box \neg \varphi) \to \Diamond (\varphi \wedge \psi) & \textsf{Def} \ \Diamond \\ 7 & & (\Box \psi \wedge \neg \Box \neg \varphi) \to \neg (\Box \psi \to \Box \neg \varphi) & \textsf{PL} \\ 8 & & (\Box \psi \wedge \neg \Box \neg \varphi) \to \Diamond (\varphi \wedge \psi) & \textsf{PL} \ 6, 7\\ 9 & & (\Box \psi \wedge \Diamond \varphi) \to (\Box \psi \wedge \neg \Box \neg \varphi) & \textsf{Def} \ \Diamond\\ 10 & & (\Diamond \varphi \wedge \Box \psi) \to (\Box \psi \wedge \Diamond \varphi) & \textsf{PL} \\ 11 & & (\Diamond \varphi \wedge \Box \psi) \to \Diamond (\varphi \wedge \psi) & \textsf{PL} \ 8, 9, 10\\ \end{array} \]
7.2 Normal Modal Logics
We will focus on extensions of the minimal modal logic that result from \(\textsf{K}\) when we supplement its axioms with substitution instances of certain modal axioms.
A normal modal \(\Sigma\) logic is an axiom system, which results from \(\textsf{K}\) when we add to its axioms all substitution instances of further modal axioms.
The normal modal logic \(\textsf{KT}\) extends the minimal normal modal logic \(\textsf{K}\) with all substitution instances of the axiom: \[\tag{\textsf{T}} \Box p \to p \] We write \(\vdash_{\textsf{KT}} \varphi\) to indicate that \(\varphi\) is a theorem of \(\textsf{KT}\).
Two more notable normal modal systems are \(\textsf{S4}\) and \(\textsf{S5}\), respectively.
The normal modal logic \(\textsf{S4}\) extends the minimal normal modal logic \(\textsf{KT}\) with all substitution instances of the axiom:
\[\tag{\textsf{4}} \Box p \to \Box \Box p \] We write \(\vdash_{\textsf{S4}} \varphi\) to indicate that \(\varphi\) is a theorem of \(\textsf{S4}\).
The normal modal logic \(\textsf{S5}\) extends the minimal normal modal logic \(\textsf{S4}\) with all substitution instances of the axiom:
\[\tag{\textsf{5}} \Diamond p \to \Box \Diamond p \] We write \(\vdash_{\textsf{S5}} \varphi\) to indicate that \(\varphi\) is a theorem of \(\textsf{S5}\).
The axioms below are interderivable from their modal duals:
| Axiom | Dual | ||
|---|---|---|---|
| \(\textsf{T}\) | \(\Box p \to p\) | \(p \to \Diamond p\) | \(\textsf{T}_\Diamond\) |
| \(\textsf{B}\) | \(p \to \Box \Diamond p\) | \(\Diamond \Box p \to p\) | \(\textsf{B}_\Diamond\) |
| \(\textsf{4}\) | \(\Box p \to \Box \Box p\) | \(\Diamond \Diamond p \to \Diamond p\) | \(\textsf{4}_\Diamond\) |
| \(\textsf{5}\) | \(\Diamond p \to \Box \Diamond p\) | \(\Diamond \Box p \to \Box p\) | \(\textsf{5}_\Diamond\) |
Consider the interderivability of \(\textsf{T}_\Diamond\) from \(\textsf{T}\):
\(\textsf{KT} \vdash \textsf{T}_\Diamond\)
\[ \begin{array}{lllll} 1 & & \Box \neg p \to \neg p & T[\neg p/p]\\ 2 & & \neg \neg p \to \neg \Box \neg p & \text{PL} \ 1\\ 3 & & \neg \neg p \to \Diamond p & \text{Def} \ \Diamond \ 2 \\ 4 & & p \to \Diamond p & \text{PL} \ 3 \\ \end{array} \]
\(\textsf{KT}_\Diamond \vdash \textsf{T}\)
\[ \begin{array}{lllll} 1 & & \neg p \to \Diamond \neg p & T_\Diamond[\neg p/p]\\ 2 & & \neg p \to \neg \Box \neg \neg p & \text{Def} \ \Diamond \ 1 \\ 3 & & \neg \neg \Box \neg \neg p \to \neg \neg p & \text{PL} \ 2 \\ 4 & & \Box \neg \neg p \to \neg \neg p & \text{PL} \ 3 \\ 5 & & p \to \neg \neg p & \text{PL} \\ 6 & & \Box p \to \Box \neg \neg p & \text{RK} \ 5 \\ 7 & & \Box p \to p & \text{PL} \ 4, 6 \\ \end{array} \]
The equivalence proof is completely parallel in all other cases.
7.2.1 Landscape of normal modal systems
We are in a position to compare the deductive strength of different normal modal systems. In what follows, we aim to develop an overview of the landscape of normal modal systems for propositional modal logic.
A modal system \(\Sigma\) extends another modal system \(\Delta\), written \(\Delta \sqsubseteq \Sigma\), if, and only if, every theorem of \(\Delta\) is a theorem of \(\Sigma\). Or, in other words, for every formula \(\varphi\) of \(\mathcal{L}^\Box\), \[ \text{If} \ \vdash_{\Delta} \varphi \ \text{then} \ \vdash_{\Sigma} \varphi \] A modal system \(\Sigma\) is a proper extension of \(\Delta\), written \(\Delta \sqsubset \Sigma\) if, and only if, \(\Delta \sqsubseteq \Sigma\) but \(\Sigma \not \sqsubseteq \Delta\).
Here is a graphical representation of some of the relations in which eleven normal modal systems stand to. each other. Each edge connects a modal system with a proper extension located above in the diagram.
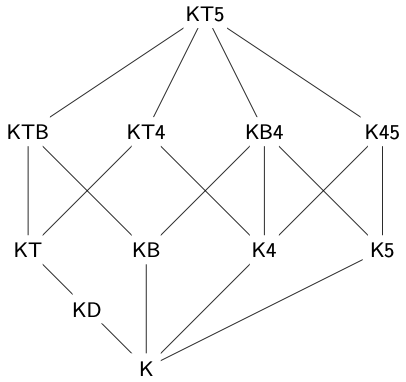
There are two main techniques we use in order to justify the diagram. To argue that a modal system \(\Sigma\) extends a system \(\Delta\), we argue that every axiom of \(\Delta\) is a theorem of \(\Sigma\).
Proposition 7.8 \(\Delta \sqsubseteq \Sigma\) if \(\Sigma\) proves every axiom of \(\Delta\).
Proof. Since \(\Delta\) and \(\Sigma\) share the same rules of inference, if every axiom of \(\Delta\) is a theorem of \(\Sigma\), then every theorem of \(\Delta\) is a theorem of \(\Sigma\).
\(\blacksquare\)
\(\textsf{KD} \sqsubseteq \textsf{KT}\)
This is because \(\vdash_{\textsf{KT}} \Box \varphi \to \Diamond \varphi\). \[ \begin{array}{lllll} 1 & & \Box \varphi \to \varphi & T[\varphi/p] \\ 2 & & \varphi \to \Diamond \varphi & T_\Diamond[\varphi/p]\\ 3 & & \Box \varphi \to \Diamond \varphi & PL \ 1, 2\\ \end{array} \]
There is a semantic counterpart to this observation. We will eventually observe that each normal modal system characterizes the set of validities in a certain class of frames. In fact, each node in the earlier diagram corresponds to a class of formulas valid in a specific class of frames:

A modal system \(\Sigma\) is sound with respect to a class of frames \(\mathcal{C}\) if, and only if, for every formula \(\varphi\) of \(\mathcal{L}^\Box\), \(\vdash_{\Sigma} \varphi\) only if \(\models_{\mathcal{C}} \varphi\).
We will see that the normal modal systems \(\textsf{KT}\) and \(\textsf{KD}\) are sound and complete with respect to the class of reflexive and serial frames, respectively. That means that the theorems of \(\textsf{KT}\) are exactly those formulas that are valid in all reflexive frames. And the theorems of \(\textsf{KD}\) are the formulas that are valid in all serial frames. Now:
Proposition 7.9 Every reflexive frame is serial.
That means that if a formula is valid in all serial frames, then it will be valid in all reflexive frames. The soundness and completeness theorems for \(\textsf{KD}\) and \(\textsf{KT}\) will deliver a semantic route to the conclusion that every theorem of \(\textsf{KD}\) is a theorem of \(\textsf{KT}\) .
On the other hand, the fact that \(\textsf{T}\) defines the class of reflexive frames suggests a semantic argument for the conclusion that \(\textsf{KD}\) does not extend \(\textsf{KT}\) .
Proposition 7.10 If every theorem of \(\Sigma\) is valid in every frame in \(\mathcal{C}\), then \(\Delta\not \sqsubseteq \Sigma\) if not every axiom of \(\Delta\) is valid in every frame in \(\mathcal{C}\).
Proof. If an axiom \(\varphi\) of \(\Delta\) is not valid in every frame in \(\mathcal{C}\), then \(\varphi\) is not a theorem of \(\Sigma\). That means that not every theorem of \(\Delta\) is a theorem of \(\Sigma\).
\(\blacksquare\)
Since the theorems of \(\textsf{KD}\) are valid in all serial frames, the observation that \(\Box p \to p\), which is an axiom of \(\textsf{KT}\) , is not valid in some serial frames tells us that \(\textsf{KT}\) is a proper extension of \(\textsf{KD}\) .
\(\textsf{KT} \not \sqsubseteq \textsf{KD}\)
This is because \(\Box p \to p\) is not valid in every serial frame. To that purpose, consider the model based on a serial frame depicted below.
\((W, R, V), w_1 \nVdash \Box p \to p\)
We may similarly use the fact that axiom 4 is not valid in every reflexive and symmetric frame to establish that some theorems of \(\textsf{KB5}\) are not theorems of \(\textsf{KTB}\).
\(\textsf{KB5} \not \sqsubseteq \textsf{KTB}\)
This is because \(\Diamond p \to \Box \Diamond p\) is not valid in every reflexive and symmetric frame. To that purpose, consider the model based on a reflexive and symmetric frame depicted below.
\((W, R, V), w_1 \nVdash \Diamond p \to \Box \Diamond p\)
Where should we locate \(\textsf{KB5}\) in the diagram? We now argue that \(\textsf{KB4}\) and \(\textsf{KB5}\) are mutual extensions of each other, which is the reason we do not have a further node for \(\textsf{KB5}\) in the diagram:
\(\textsf{KB4} \sqsubseteq \textsf{KB5}\)
This is because \(\vdash_{\textsf{KB5}} \Box \varphi \to \Box \Box \varphi\).
\[ \begin{array}{lllll} 1 & & \Box \varphi \to \Box \Diamond \Box \varphi & \textsf{B}[\Box \varphi/p]\\ 2 & & \Diamond \Box \varphi \to \Box \varphi & \textsf{5}_\Diamond [\varphi/p]\\ 3 & & \Box \Diamond \Box \varphi \to \Box \Box \varphi & \textsf{RK} \ 2 \\ 4 & & \Box \varphi \to \Box \Box \varphi & \textsf{PL} 1, 3\\ \end{array} \]
\(\textsf{KB5} \sqsubseteq \textsf{KB4}\)
This is because \(\vdash_{\textsf{KB4}} \Diamond \varphi \to \Box \Diamond \varphi\).
\[ \begin{array}{lllll} 1 & & \Diamond \varphi \to \Box \Diamond \Diamond \varphi & \textsf{B}[\diamond \varphi/p]\\ 2 & & \Diamond \Diamond \varphi \to \Diamond \varphi & \textsf{4}_\Diamond[\varphi/p] \\ 3 & & \Box \Diamond \Diamond \varphi \to \Box \Diamond \varphi & \textsf{RK} \ 2\\ 4 & & \Diamond \varphi \to \Box \Diamond \varphi & \textsf{PL} \ 1, 3\\ \end{array} \]
\(\textsf{KB4} = \textsf{KB5}\)
This is an immediate consequence of the last two examples.