6 Basic Language

We introduce the syntax and semantics of the modal propositional language.

6.1 Syntax

We first specify the syntax of a modal propositional language $\mathcal{L}^\Box$:

Modal Propositional Language

We choose a stock of propositional variables or atoms:

\[ AT := p, q, r, \cdots \]

We define the formulas of a propositional language $\mathcal{L}^\Box$ recursively:

\[ \varphi ::= AT \ | \ \neg \varphi \ | \ (\varphi \to \psi) \ | \ \Box \varphi \]

Here is how to read the last line:

All atoms are formulas.
If $\varphi$ is a formula, then $\neg \varphi$ is a formula.
If $\varphi$ and $\psi$ are formulas, then $(\varphi \to \psi)$ is a formula.
If $\varphi$ is a formula, then $\Box \varphi$ is a formula.

That is, a string of symbols is a formula if, and only if, it arises from atoms from negation, conditional, and the box in a finite number of steps.

We now define further connectives and $\Diamond$ in terms of $\neg$, $\to$ and $\Box$:

Definition 6.1 (Connectives) \[ \begin{array}{lll} \top & := & (p \to p)\\ \bot & := & \neg \top \\ (\varphi \vee \psi) & := & (\neg \varphi \to \psi)\\ (\varphi \wedge \psi) & := & \neg (\varphi \to \neg \psi)\\ (\varphi \leftrightarrow \psi) & := & (\varphi \to \psi) \wedge (\psi \to \varphi)\\ \Diamond \varphi & := & \neg \Box \neg \varphi\\ \end{array} \]

The inductive definition of formula vindicates a principle of induction for formulas.

Induction on the Complexity of Formulas

Given a condition $\Phi(\alpha)$ on formulas of $\mathcal{L}^\Box$, if

all atoms satisfy $\Phi(\alpha)$,
whenever a formula $\varphi$ satisfies $\Phi(\alpha)$, $\neg \varphi$ satisfies $\Phi(\alpha)$,
whenever two formulas $\varphi$ and $\psi$ satisfy $\Phi(\alpha)$, $(\varphi \to \psi)$ satisfies $\Phi(\alpha)$, and
whenever a formula $\varphi$ satisfies $\Phi(\alpha)$, $\Box \varphi$ satisfies $\Phi(\alpha)$,

then every formula satisfies $\Phi(\alpha)$

We now generalize uniform substitution for the modal propositional language.

Uniform Substitution

Given a formula $\varphi$ whose propositional variables are among $p_1, \dots, p_n$ and formulas $\psi_1, \dots, \psi_n$, define $\varphi[\psi_1/p_1, ..., \psi_n/p_n]$ inductively:

If $\varphi$ is $p_i$, $\varphi[\psi_1/p_1, ..., \psi_n/p_n]$ is $\psi_i$.
If $\varphi$ is $\neg \chi$, $\varphi[\psi_1/p_1, ..., \psi_n/p_m]$ is $\neg \chi[\psi_1/p_1, ..., \psi_n/p_m]$.
If $\varphi$ is $(\chi \to \rho)$, then $\varphi[\psi_1/p_1, ..., \psi_n/p_n]$ is $(\chi[\psi_1/p_1, ..., \psi_n/p_n]\to \rho[\psi_1/p_1, ..., \psi_n/p_n])$.
If $\varphi$ is $\Box \chi$, $\varphi[\psi_1/p_1, ..., \psi_n/p_m]$ is $\Box \chi[\psi_1/p_1, ..., \psi_n/p_m]$.

6.2 Possible Worlds Semantics

We use possible worlds models to interpret the modal propositional language.

Possible Worlds Model

A possible worlds model $M$ for $\mathcal{L}^\Box$ is a structure $(W, R, V)$ where:

$W$ is a non-empty set of worlds
$R$ is a binary accessibility relation on $W$
$V$ maps each propositional variable $p$ to a set of worlds $V(p) \subseteq W$.

Notation

When $Ruv$, sometimes written $uRv$, we will write that $v$ is accessible from $u$ or that $u$ sees $v$. The accessibility relation represents a relation of relative possibility: $v$ is accessible from $u$ corresponds to the claim that $v$ is possible relative to $u$.

$V$ maps a propositional variable $p$ to a set of worlds $w$ at which $p$ is true. So, when $w \in V(p)$, we will write that $p$ is true at $w$.

One way to think of the assignment $V$ is as a specification of the set of worlds at which each propositional variable is true.

We will use directed graphs to represent possible worlds models.

How to Use a Graph to Represent a Possible Worlds Model

Here is a depiction of a possible worlds model of the form $(W, R, V)$ where:

$W = \{w_1, w_2, w_3, w_4\}$
$R = \{(w_1, w_2), (w_2, w_3), (w_3, w_4), (w_1, w_4), (w_1, w_3), (w_2, w_2)\}$
$V(p) = \{w_3, w_4\}$; $V(q) = \{w_2, w_4\}$

Each node corresponds to a possible world in the model.
The accessibility relation relates one world to another when there is an arrow that points from the first to the second.
The graph records the propositional variables that are true at each world according to the assignment $V$. If a propositional variable is not written at a node of the diagram, then the variable is not true at that world on the valuation depicted by the graph.

We do not have the means yet to ask whether a complex formula $\varphi$ is true at a world in a model. To that purpose, we provide a recursive definition of a semantic relation between a world $w$ in a model $M$ and a formula $\varphi$.

Truth at a World

We define what is for a formula $\varphi$ to be true at a world $w$ in a possible worlds model $M$, which we write: $M, w \Vdash \varphi$: \[ \begin{array}{lll} M, w \Vdash p & \text{iff} & w \in V(p)\\ M, w \Vdash \neg \varphi & \text{iff} & M, w \nVdash \varphi\\ M, w \Vdash (\varphi \to \psi) & \text{iff} & M, w \nVdash \varphi \ \text{or} \ M, w \Vdash \psi\\ M, w \Vdash \Box \varphi & \text{iff} & \text{for every} \ u \in W \ \text{such that} \ Rwu, \ M, u \Vdash \varphi\\ \end{array} \]

Given the usual defintion of $\Diamond$ in terms of $\Box$, we find that \[ \begin{array}{lll} M, w \Vdash \Diamond \varphi & \text{iff} & \text{for some} \ u \in W \ \text{such that} \ Rwu, \ M, u \Vdash \varphi\\ \end{array} \]

We may return to the example above to explain how to compute the truth value of a formula at a world in a model.

Example

Evaluate each of the complex modal formulas given below at each possible world in the model:

$p \to (p \to q)$

This formula is true at worlds $w_1$, $w_2$ $w_3$ but not at $w_4$.
- $M, w_4 \nVdash p \to (p \to q)$ because $M, w_4 \Vdash p$, yet $M, w_4 \nVdash p \to q$. That is, $p$ is true at $w_4$ but $p\to q$ is not true at $w_4$.

$\Box p$

This formula is true exactly at worlds $w_3$ and $w_4$.
- $M, w_1 \nVdash \Box p$ because $Rw_1w_2$ and $M, w_2 \nVdash p$. That is, $\Box p$ is not true at $w_1$ because $p$ is not true at $w_2$, which is world accessible from $w_1$.
- $M, w_2 \nVdash \Box p$ because $Rw_2w_2$ and $M, w_2 \nVdash p$.
- $M, w_3 \Vdash \Box p$ because for every $u \in W$, if $Rw_3 u$, then $M, u \Vdash p$. That is $p$ is true at all worlds that are accessible from $w_3$, namely, $w_4$.
- $M, w_4 \Vdash \Box p$ because for every $u \in W$, if $Rw_4 u$, then $M, u \Vdash p$. That is $p$ is true at all worlds that are accessible from $w_4$ which in this case are none.

$\Diamond \Box p$

This formula is true exactly at worlds $w_1$, $w_2$ and $w_3$ but not at $w_4$.
- $M, w_1 \Vdash \Diamond \Box p$ because $Rw_1w_3$ and $M, w_3 \Vdash \Box p$. That is, $\Box p$ is true at some world that is accessible from $w_1$, namely, $w_3$.
- $M, w_2 \Vdash \Diamond \Box p$ because $Rw_2w_3$ and $M, w_3 \Vdash \Box p$.
- $M, w_3 \nVdash \Diamond \Box p$ because because there is no $u\in W$ such that $Rw_3u$ and $M, u \Vdash \Box p$. Since no world is accessible from $w_3$, $\Box p$ is not true at a world that is accessible from $w_3$.
- $M, w_4 \nVdash \Diamond \Box p$ because there is no $u\in W$ such that $Rw_4u$ and $M, u \Vdash \Box p$.

$\Box (q \to p)$

This formula is true exactly at worlds $w_3$ and $w_4$.
- $M, w_1 \nVdash \Box (q \to p)$ because $Rw_1w_2$ and $M, w_2 \nVdash q \to p$. That is, $q \to p$ is not true at every world that is accessible from $w_1$, e.g., it is not true at $w_3$.
- $M, w_2 \nVdash \Box (q \to p)$ because $Rw_2w_2$ and $M, w_2 \nVdash q \to p$.
- $M, w_3 \Vdash \Box (q \to p)$ because for every $u \in W$, if $Rw_3 u$, then $M, u \Vdash q \to p$. That is $q \to p$ is true at all worlds that are accessible from $w_3$, namely, $w_4$.
- $M, w_4 \Vdash \Box (q \to p)$ because for every $u \in W$, if $Rw_4 u$, then $M, u \Vdash q \to p$. That is $q \to p$ is true at all worlds that are accessible from $w_4$ which in this case are none.

We finally define what is for a formula to be true at a model.

Truth at a Model

A formula $\varphi$ to be true in a possible worlds model $M$, which we write $M \Vdash \varphi$ if, and only if, for all $w\in W$, $M, w \Vdash \varphi$.

We now return to the example above.

Example

Here is how to evaluate complex modal formulas in the model:

$\neg p \to \Diamond p$

This formula is true in the model because it is true at all possible worlds.
- $\neg p \to \Diamond p$ is true at $w_3$ and $w_4$ because $\neg p$ is not true at either world.
- $\neg p \to \Diamond p$ is true at $w_1$ and $w_2$ because $\Diamond p$ is true at both worlds: $\Diamond p$ is true at $w_1$ because $Rw_1w_3$ and $p$ is true at $w_3$, and $\Diamond p$ is true at $w_2$ because $Rw_2w_3$ and $p$ is true at $w_3$.

$p \to \Box q$

This formula is true in the model because it is true at all possible worlds.
- $p \to \Box q$ is true at $w_1$ and $w_2$ because $p$ is not true at either world.
- $p \to \Box q$ is true at $w_3$ and $w_4$ because $\Box q$ is true at both worlds: $\Box q$ is true at $w_3$ because $q$ is true at all worlds accessible from $w_3$, namely, $w_4$; $\Box q$ is true at $w_4$ because $q$ is true at all worlds accessible from $w_4$, namely, none.

6.2.1 Frames

We make a distinction between two ingredients for a possible worlds model. One is the frame of the model, which consists of a set of worlds $W$ and a relation $R$ on $W$, and the other is the assignment $V$ based on that frame.

Frame

A frame $F$ for $\mathcal{L}^\Box$ is an ordered pair $(W, R)$ where:

$W$ is a non-empty set of worlds, and
$R$ is a binary accessibility relation on $W$

A model $M$ is based on a frame $F = (W, R)$ if, and only if, there is an assignment $V$ such that $M = (F, V)$. That is, $M = (W, R, V)$.

For a formula $\varphi$ of $\mathcal{L}^\Box$ to be valid in a frame is to be true in every model based on that frame, that is, to be true at every world of every model based on that frame.

Validity

A formula $\varphi$ is valid in a frame $(W, R)$, written $(W, R) \models \varphi$, if, and only if, $\varphi$ is true in every model $(W, R, V)$ based on the frame $(W, R)$.

That is, the formula remains true across assignments no matter what sets of worlds we assign to what propositional variables.

A formula $\varphi$ is valid, written $\models \varphi$, if, and only if, $\varphi$ is valid in every frame $(W, R)$.

Example

Here are two formulas of $\mathcal{L}^\Box$ that are valid in every frame:

$\Diamond (p \vee q) \leftrightarrow (\Diamond p \vee \Diamond q)$
$\Box (p \wedge q) \leftrightarrow (\Box p \wedge \Box q)$

The modal operators $\Diamond$ and $\Box$ distribute over disjunction and conjunction, respectively. These formulas are true at every world of every possible worlds model, which means that they are true in every model based on every frame.

Here are, on the other hand, two formulas of $\mathcal{L}^\Box$ that are not valid in every frame:

$\Diamond (p \wedge q) \leftrightarrow (\Diamond p \wedge \Diamond q)$
$\Box (p \vee q) \leftrightarrow (\Box p \vee \Box q)$

For a counterexample to the validity of the first formula, consider the model below:

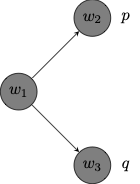
Notice that $\Diamond p \wedge \Diamond q$ is true at $w_1$ because each conjunct is true at $w_1$:

$\Diamond p$ is true at $w_1$ because $p$ is true at $w_2$, which is accessible from $w_1$
$\Diamond q$ is true at $w_1$ because $q$ is true at $w_3$, which is accessible from $w_1$

Yet, $\Diamond (p \wedge q)$ is false at $w_1$ since $p \wedge q$ is not true at any world accessible from $w_1$.

The model doubles as a counterexample to the validity of the second formula:

Notice that $\Box (p \vee q)$ is true at $w_1$ because $p \vee q$ is true at every world accessible from $w_1$:

$p \vee q$ is true at $w_2$ because $p$ is true at $w_2$.
$p \vee q$ is true at $w_3$ because $q$ is true at $w_3$.

However, $\Box p \vee \Box q$ is not true at $w_1$ because neither $\Box p$ nor $\Box q$ is true at $w_1$.

$\Box p$ is not true at $w_1$ because $p$ is not true at $w_3$, which is accessible from $w_1$.
$\Box q$ is not true at $w_1$ because $q$ is not true at $w_2$, which is accessible from $w_1$.

Proposition 6.1 The formula $\Box (p \to q) \to (\Box p \to \Box q)$ is valid in every frame.

Let $(W, R)$ be a frame, and let $(W, R, V)$ be a model based on that frame. Let $w\in W$ be a world such that $(W, R, V), w \Vdash \Box(p \to q)$. Suppose further that $(W, R, V), w \Vdash \Box p$. We set out to argue that $(W, V, R), w \Vdash \Box q$. For let $u \in W$ be such that $Rwu$. By assumption, $(W, R, V), u \Vdash p \to q$ and $(W, R, V), u \Vdash p$. It follows that $(W, R, V), u \Vdash q$. Generalizing, for every $u \in W$ such that $Rwu$, $W, R, V), u \Vdash q$, whence $(W, R, V), w \Vdash \Box q$.

$\blacksquare$

We will often restrict attention to a class of frames and ask which formulas are valid in all and only those frames in the class.

Validity in a Class of Frames

A formula $\varphi$ is valid in a class of frames $\mathcal{C}$, written $\models_{\mathcal{C}} \varphi$ if, and only if, $\varphi$ is valid in every frame $(W, R)$ in the class $\mathcal{C}$.

Proposition 6.2 Each formula listed below is valid in a frame if the accessibility relation satisfies the relevant condition.

	Formula	Condition on $R$
$\textsf{T}$	$\Box p \to p$	reflexive on $W$
$\textsf{B}$	$p \to \Box \Diamond p$	symmetric on $W$
$\textsf{4}$	$\Box p \to \Box \Box p$	transitive on $W$
$\textsf{5}$	$\Diamond p \to \Box \Diamond p$	euclidean on $W$

Proof. We look at each case in turn:

$\textsf{T}$ is valid in all reflexive frames.

Let $(W, R, V)$ be a model based on a reflexive frame $(W, R)$. Given $w \in W$, suppose $(W, R, V), w \Vdash \Box p$, which means that for all $u\in W$, if $Rwu$, then $u \in V(p)$. Since $R$ is reflexive, $Rww$ and $w \in V(p)$. So, $(W, R, V), w \Vdash \Box p$ and $(W, R, V), w \Vdash \Box p \to p$. Generalizing, we conclude $(W, R, V) \Vdash \Box p \to p$.

$\textsf{B}$ is valid in all symmetric frames.

Let $(W, R, V)$ be a model based on a symmetric frame $(W, R)$. Given $w \in W$, suppose $(W, R, V), w \Vdash p$, which means that $w \in V(p)$. Let $u\in W$ be such that $Rwu$. Since $R$ is symmetric on $W$, $Rwu$, which means that $(W, R, V), u \Vdash \Diamond p$. Generalizing, for every $u\in W$, if $Rwu$, $(W, R, V), u \Vdash \Diamond p$. We conclude that $(W, R, V), w \Vdash \Box \Diamond p$ and $(W, R, V), w \Vdash p \to \Box \Diamond p$. Generalizing again, we find $(W, R, V) \Vdash p \to \Box \Diamond p$.

$\textsf{4}$ is valid in all transitive frames.

Let $(W, R, V)$ be a model based on a transitive frame $(W, R)$. Given $w \in W$, suppose $(W, R, V), w \Vdash \Box p$, which means that for all $u\in W$, if $Rwu$, then $u \in V(p)$. Let $u\in W$ be such that $Rwu$. We want to verify that $(W, R, V), u \Vdash \Box p$. For let $t\in W$ be such that $Rut$. Since $R$ is transitive on $W$, $Rwt$, which means that $t\in V(p)$ and $(W, R, V), t \Vdash p$. Generalizing, for every $t\in W$, if $Rut$, $(W, R, V), t \Vdash p$. We conclude that $(W, R, V), u \Vdash \Box p$ and $(W, R, V), w \Vdash \Box \Box p$. So, $(W, R, V), w \Vdash \Box p \to \Box \Box p$. Generalizing again, we infer $(W, R, V) \Vdash \Box p \to \Box \Box p$.

$\textsf{5}$ is valid in euclidean frames.

Let $(W, R, V)$ be a model based on a euclidean frame $(W, R)$. Given $w \in W$, suppose $(W, R, V), w \Vdash \Diamond p$, which means that for some $u\in W$ such that $Rwu$, we have $u \in V(p)$. Let $t \in W$ be such that $Rwt$. Since $R$ is euclidean, $Rtu$, which means that $(W, R, V), t \Vdash \Diamond p$. Generalizing, we find that for every $t\in W$, if $Rut$, $(W, R, V), t \Vdash \Diamond p$. So, $(W, R, V), w \Vdash \Box \Diamond p$. So, $(W, R, V), w \Vdash \Diamond p \to \Box \Diamond p$. Generalizing again, we infer $(W, R, V) \Vdash \Diamond p \to \Box \Diamond p$.

$\blacksquare$

6.2.2 Frame Definability

The success of the possible worlds semantics is connected to the fact that it sheds new light on modal principles via systematic correspondences between the validity of those principles and certain structural features of the modal accesssibility relation $R$ on a set of worlds $W$ in a frame $(W, R)$.

Proposition 6.3 Each formula listed below is valid in a frame only if the accessibility relation satisfies the relevant condition.

	Formula	Condition on $R$
$\textsf{T}$	$\Box p \to p$	reflexive on $W$
$\textsf{B}$	$p \to \Box \Diamond p$	symmetric on $W$
$\textsf{4}$	$\Box p \to \Box \Box p$	transitive on $W$
$\textsf{5}$	$\Diamond p \to \Box \Diamond p$	euclidean on $W$

Proof. We provide two styles of argument for each case. One targets the contrapositive, while the other consists of a direct proof of the conditional.

$\textsf{T}$ is only valid in reflexive frames.

If $R$ is not reflexive on $W$ in a frame $(W,R)$, then there is an assignment $V$ and a world $w\in W$ such that $(W, R, V), w \nVdash \Box p \to p$.

Suppose $R$ is not reflexive on $W$ in a frame $(W,R)$. That means that there is a world $w \in R$ such that $\neg Rww$. Define $V$ to let $V(p) = W \setminus \{w\}$. On the one hand, $(W, R, V), w \Vdash \Box p$ because $p$ is true at any world accessible from $w$. On the other hand, $(W, R, V), w \nVdash p$ because $w \notin V(p)$. So, $(W, R, V), w \nVdash \Box p \to p$
If $(W, R) \models \Box p \to p$, then $R$ is reflexive on $W$.

Suppose $(W, R) \models \Box p \to p$. Fix $w \in W$ and consider the assignment $V(p) = \{u\in W: Rwu\}$. It follows that $(W, R, V), w \Vdash \Box p$. Since $(W, R, V), w \Vdash \Box p \to p$, we infer $w \in V(p)$, which means that $Rww$.

$\textsf{B}$ is only valid in symmetric frames.

If $R$ is not symmetric on $W$ in a frame $(W,R)$, then there is an assignment $V$ and a world $w\in W$ such that $(W, R, V), w \nVdash p \to \Box \Diamond p$.

Suppose $R$ is not symmetric on $W$ in a frame $(W,R)$. That means that there are two worlds $w, u \in R$ such that $Rwu$ and $\neg Ruw$. Define $V$ to let $V(p) = \{w\}$. On the one hand, $(W, R, V), w \Vdash p$ because $w \in V(p)$. On the other hand, $(W, R, V), w \nVdash \Box \Diamond p$ because $Rwu$ and $(W, R, V), u \nVdash \Diamond p$. The reason for this is that $\neg Ruw$ and $w$ is the only world at which $p$ is true in the model.
If $(W, R) \models p \to \Box \Diamond p$, then $R$ is symmetric on $W$.

Suppose $(W, R) \models p \to \Box \Diamond p$. Fix $w, u \in W$ and consider the assignment $V(p) = \{w\}$. It follows that $(W, R, V), w \Vdash p$. Since $(W, R, V), w \Vdash \Box \Diamond p$ and $Rwu$, we infer that $(W, R, V), u \Vdash \Diamond p$, which means that $Ruw$ as $V(p)= \{w\}$. Generalizing, we conclude that $R$ is symmetric on $W$.

$\textsf{4}$ is only valid in transitive frames.

If $R$ is not transitive on $W$ in a frame $(W,R)$, then there is an assignment $V$ and a world $w\in W$ such that $(W, R, V), w \nVdash \Box p \to \Box \Box p$.

Suppose $R$ is not transitive on $W$ in a frame $(W,R)$. That means that there are three worlds $w, u, t \in R$ such that $Rwu$ and $Rut$ but $\neg Rwt$. Define $V$ to let $V(p) = \{v\in W: Rwv\}$. On the one hand, $(W, R, V), w \Vdash \Box p$ because $v\in V(p)$ for every $v\in W$ such that $Rwv$. On the other hand, $(W, R, V), w \nVdash \Box \Box p$ because $Rwu$ and $(W, R, V), u \nVdash \Box p$. The reason for this is that $Rut$ and $t\notin V(p)$ since $\neg Rwt$.
If $(W, R) \models \Box p \to \Box \Box p$, then $R$ is transitive on $W$.

Suppose $(W, R) \models \Box p \to \Box \Box p$. Fix $w, u, t \in W$ and assume $Rwu$ and $Rut$. Consider an assignment $V$ on which $V(p) = \{v: Rwv \}$. If $(W, R, V), w \Vdash \Box p$, then since $Rwu$ and $(W, R), w \vDash \Box p \to \Box \Box p$, $(W, R, V), w \Vdash \Box \Box p$ and $(W, R), u \vDash \Box p$. So, since $Rut$, $(W, R), t \vDash p$. That means that $u\in V(p)$ and, by definition of $V$, $Rwt$.

$\textsf{5}$ is only valid in euclidean frames.

If $R$ is not euclidean on $W$ in a frame $(W,R)$, then there is an assignment $V$ and a world $w\in W$ such that $(W, R, V), w \nVdash \Diamond p \to \Box \Diamond p$.

Suppose $R$ is not euclidean on $W$ in a frame $(W,R)$. That means that there are three worlds $w, u, t \in R$ such that $Rwu$ and $Rwt$ but $\neg Rut$. Define $V$ to let $V(p) = \{t\}$. On the one hand, $(W, R, V), w \Vdash \Diamond p$ because $t\in V(p)$ and $Rwt$. On the other hand, $(W, R, V), w \nVdash \Box \Diamond p$ because $Rwu$ and $(W, R, V), t \nVdash \Diamond p$, since $\neg Rut$.
If $(W, R) \models \Box p \to \Box \Box p$, then $R$ is euclidean on $W$.

Suppose $(W, R) \models \Diamond p \to \Box \Diamond p$. Fix $w, u \in W$ and consider the assignment $V(p) = \{u\}$. It follows that $(W, R, V), w \Vdash \Diamond p$. Since $(W, R, V), w \Vdash \Box \Diamond p$ and $Rwu$, we infer that $(W, R, V), u \Vdash \Diamond p$, which means that $Ruw$ as $V(p)= \{w\}$. Generalizing, we conclude that $R$ is euclidean on $W$.

$\blacksquare$

Let us make precise the the observation that each of the formulas discussed characterizes a class of frames.

Modal Definability

A formula $\varphi$ of $\mathcal{L}^\Box$ modally defines a class of frames $\mathcal{C}$ iff for all frames $(W, R)$,

\[ \begin{array}{lll} (W, R) \models \varphi & \text{iff} & (W, R) \in \mathcal{C} \end{array} \]

Each of the formulas discussed above defines the class of frames in which the accessibility relation satisfies the relevant formal condition. That is,

$\textsf{T}$ modally defines the class of reflexive frames
$\textsf{B}$ modally defines the class of symmetric frames
$\textsf{4}$ modally defines the class of transitive frames
$\textsf{5}$ modally defines the class of euclidean frames

The expressive power of propositional modal logic is measured by the ability to make distinctions. The language affords us the means to distinguish reflexive from non-reflexive frames in terms of the validity of the formula $\Box p \to p$. Likewise, we have the means to make distinctions between symmetric and non-symmetric frames or between transitive and non-transitive frames.

First-order languages are able to make similar distinctions. Given a first-order language with a binary relational predicate $R$ as a non-logical predicate, we are in a position to specify first-order formulas that characterize different classes of frames:

Frames	Modal Definability	First-Order Definability
Reflexive	$\Box p \to p$	$\forall x \ Rxx$
Symmetric	$p \to \Box \Diamond p$	$\forall x \forall y (Rxy \to Ryx)$
Transitivity	$\Box p \to \Box \Box p$	$\forall x \forall y \forall z (Rxy \wedge Ryz \to Rxz)$
Euclidean	$\Diamond p \to \Box \Diamond p$	$\forall x \forall y \forall z (Rxy \wedge Rxz \to Ryz)$

One may now compare the expressive power of modal and first-order logic. Even if the class of reflexive, symmetric, and transitive frames are each modal and first-order definable, one may wonder whether every class of formulas defined by a first-order formula is modally definable and, vice versa, whether every modally definable frame is first-order definable.

The answer to both questions is ‘no’. Some formulas of $\mathcal{L}^\Box$ are able to modally define classes of frames that are not first-order definable, and some classes of frames that are first-order definable are not modally definable by a formula of $\mathcal{L}^\Box$.

Frames	Modal Definability	First-Order Definability
Irreflexive	No	$\forall x \ \neg Rxx$
Universal	No	$\forall x \forall y Rxy$
Transitive Converse Well-Founded	$\Box (\Box p \to p) \to \Box p$	No
Identity	Yes	$\forall x \forall y (Rxy \leftrightarrow x = y)$
Functional	Yes	$\forall x \forall y (Rxy \wedge Rxz \to x =y)$
Serial	Yes	$\forall x \exists y Rxy$

Converse Well-Founded

A binary relation $R$ on a set $W$ converse well-founded iff there are no infinite ascending $R$-chains of the form $x_1Rx_2 \cdots x_nRx_{n+1} \cdots$.

Proposition 6.4 The class of transitive converse well-founded frames is not first-order definable.

This is a consequence of the Compactness Theorem for first-order logic: if a set of first-order formulas $\Gamma$ is finitely satisfiable, then $\Gamma$ is finitely satisfiable.

Proof. For each natural number $n > 0$, let $\varphi_n$ be a formula according to which there is a finite $R$-chain with at least $n+1$ nodes:

\[ \varphi_n := \exists x_1 \dots \exists x_{n+1} \ (Rx_1x_2 \wedge \dots \wedge Rx_n x_{n+1}) \]For every first-order formula $\psi$, if $\psi$ is true of every converse-well-founded frame, then if $\Sigma$ is a set of formulas that requires $R$ to form a linear order, that is, be irreflexive, transitive, and connected, then \[ \Sigma \cup \{\varphi_n: n > 0\}, \psi \]is finitely satisfiable. If $\Delta$ is a finite subset of that set, then there is a largest $n$ for which $\varphi_n \in \Delta$, and a frame $(W, R)$ in which $R$ is a linear order of exactly $n$ worlds will satisfy $\Delta$. By Compactness, $\Sigma \cup \{\varphi_n: n > 0\}, \psi$ is satisfiable, which requires a frame $(W, R)$ in which $R$ is a linear order of an infinity of worlds in $W$. So, $\psi$ is satisfiable in a non-converse-well-founded frame. So, if $\psi$ is true of every converse well-founded frame, then it is true of some non-converse-well-founded frames.

$\blacksquare$

Proposition 6.5 $\Box (\Box p \to p) \to \Box p$ modally defines the class of converse well-founded frames.

Proof. We want to prove that for all frames $(W, R)$,

\[ \begin{array}{lll} (W, R) \models \Box (\Box p \to p) \to \Box p & \text{iff} & R \ \text{transitive} \ \text{and} \ \text{converse}\\ & & \text{well-founded on} \ W \end{array} \] ($\Rightarrow$) Suppose $R$ is not transitive. Then there are worlds $w, u, v\in W$ such that $wRu$ and $uRv$ but not $wRv$. In that case, let $V(p) = W \setminus \{u, v\}$ and note that $(W, R, V), w \nVdash \Box p$ and $(W, R, V), u \nVdash \Box p$. Furthermore, $(W, R, V), u \nVdash \Box p \to p$. However, by definition of $V$, if $Rwt$, then either $t =u$ or $t \in V(p)$. Either way, $(W, R, V), t \Vdash p$ and $(W, R, V), t \Vdash \Box p \to p$. So, $(W, R, V), w \Vdash \Box (\Box p \to p)$. So, $(W, R, V), w \nVdash \Box (\Box p \to p) \to \Box p$.

Now, suppose $R$ is not converse well-founded. Then there is an infinite $R$-chain $u_1 Ru_2 \dots u_nRu_{n+1} \dots$. In that case, we efine $V(p)$ to exclude every member of the $R$-chain, that is, $V(p) = W \setminus \{u_1, u_2, \dots\}$. Given some $w \in X$, we argue that $(W, R, V), w \Vdash \Box (\Box p \to p)$ even though $(W, R, V), w \nVdash \Box p$. For the former, note that $(W, R, V), u_n \nVdash \Box p$ for each member $u_n$ of the infinite $R$-chain. So, $(W, R, V), u_n \Vdash \Box p \to p$ and $(W, R, V), u_n \Vdash \Box (\Box p \to p)$ for every member $u_n$ of the infinite $R$-chain. So, $(W, R, V), u_n \nVdash \Box (\Box p \to p) \to \Box p$ for every member $u_n$ of the infinite $R$-chain.

($\Leftarrow$) Suppose $R$ is transitive and converse well-founded. Furthermore, let $(W, R, V)$ be a model based on $(W, R)$ and let $w \in W$. We now argue that $(W, R, V), w \Vdash \Box (\Box p \to p)\to \Box p$. For suppose $(W, R, V), w \nVdash \Box p$ and consider the set $X=\{u \in W: wRu \wedge u\notin V(p) \}$. We know that this set is non-empty since $(W, R, V), w \nVdash \Box p$. Since $R$ is converse well-founded, there is some $v \in X$ such that $\neg vRt$ for any $t\in X$. Otherwise, we would have an infinite $R$-chain. Since $v\in X$, we have that $(W, R, V), v \nVdash p$, despite the fact that if $vRt$, by transitivity, $wRt$ and since $t\notin X$, $(W, R, V), t \Vdash p$. So, $(W, R, V), v \Vdash \Box p$ and $(W, R, V), v \nVdash \Box p \to p$. It follows that $(W, R, V), w \nVdash \Box (\Box p \to p)$.

$\blacksquare$

6.2.3 Bisimulations

We know that first-order formulas do not discriminate between isomorphic models. The role of isomorphism in first-order logic is played by bisimulation in modal propositional logic, since modal formulas do not discriminate between bisimilar models.

Bisimulation

A bisimulation between two models $(W, R, V)$ and $(W', R', V')$ is a binary relation $E \subseteq W \times W'$ such that for all $w\in W$ forall $w' \in W'$,

if $wEw'$, then $w$ and $w'$ verify exactly the same propositional variables in each model, that is, for all propositional variable $p$, $w \in V(p)$ iff $w' \in V'(p)$.
if $wEw'$ and $Rwu$ for some $u\in W$, then there is some $u'\in W'$ such that $Rw'u'$ and $uEu'$ (the forth condition)
if $wEw'$ and $Rw'u'$ for some $u'\in W'$, then there is some $u \in W$ such that $Rwu$ and $u'Eu$ (the back condition)

If $E$ is a bisimulation between two models $(W, R, V)$ and $(W', R', V')$, we will call them bisimilar. Furthermore, if $wEw'$, we will write that the two worlds $w$ and $w'$ are bisimilar.

Example

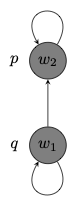
There is a bisimulation $E \subseteq W \times W'$ between the models depicted below:

$(W, R, V)$	$(W', R', V')$

$E$ relates $w_1$ to each $u_1$ and $v_2$, and $E$ relates each of $u_1$ and $v_1$ to $w_1$.

$E$ relates $w_2$ to each $u_2$ and $v_2$, and $E$ relates each of $u_2$ and $v_2$ to $w_2$.

One way to think of the situation is that $w_1$ and $w_2$ have each unfolded into two duplicate worlds $u_1$ and $v_1$ and $u_2$ and $v_2$, respectively. Notice, however, that the two models verify exactly the same formulas of propositional modal logic.

Proposition 6.6 (Invariance Lemma) If there is a bisimulation $E$ between two models $(W, R, V)$ and $(W', R', V')$, then for all $w\in W$, for all $w'\in W'$, if $wEw'$, the for every formula $\varphi$ of $\mathcal{L}^\Box$: \[ \begin{array}{lll} (W, R), w \Vdash \varphi & \text{iff} & (W', R'), w' \Vdash \varphi. \end{array} \]

Proof. The proof is by induction over the complexity of formulas.

Base Case. If $\varphi$ is a propositional variable $p$, then if $wEw'$, by clause 1 in the definition of bisimulation, $w \in V(p)$ iff $w' \in V'(p)$, which means

\[ \begin{array}{llll} (W, R, V), w \Vdash p & \text{iff} & w \in V(p) &\\ & & w' \in V'(p) & \text{Clause 1}\\ & & (W', R', V'), w' \Vdash p & \end{array} \] The Boolean cases are immediate:

Inductive Step for $\neg$:

\[ \begin{array}{llll} (W, R, V), w \Vdash \neg \varphi & \text{iff} & (W, R, V), w \nVdash \varphi & \\ & & (W', R', V'), w' \nVdash \varphi & IH \\ & & (W', R', V'), w' \Vdash \neg \varphi & \\ \end{array} \] On to the case of $\to$:

Inductive Step for $\to$:

\[ \begin{array}{llll} (W, R, V), w \Vdash \varphi \to \psi & \text{iff} & (W, R, V), w \nVdash \varphi \ \text{or} \ (W, R, V), w \Vdash \psi & \\ & & (W', R', V'), w' \nVdash \varphi \ \text{or} \ (W', R', V'), w' \Vdash \psi & IH \\ & & (W', R', V'), w' \Vdash \varphi \to \psi& \\ \end{array} \] The case for $\Box$ requires more attention:

Inductive Step for $\Box$:

\[ \begin{array}{llll} (W, R), w \Vdash \Box \varphi & \text{iff} & (W, R), u \Vdash \varphi \ \ \text{whenever} \ \ wRu & \\ & & (W', R'), u' \Vdash \varphi \ \ \text{whenever} \ \ w'R'u' & \text{Clauses 2, 3, and} \ IH\\ & & (W', R'), w' \Vdash \Box \varphi& \\ \end{array} \]

Here is a more detailed justification of the step from $(W, R), u \Vdash \varphi$ whenever $u \in W$ and $wRu$ to $(W', R'), u' \Vdash \varphi$ whenever $u' \in W'$:

Suppose $(W, R, V), u \Vdash \varphi$ whenever $u \in W$ and $wRu$. We now argue that if $wEw'$, then $(W', R', V'), u' \Vdash \varphi$ whenever $u' \in W'$ and $w'Ru'$. For if $w'R'u'$, then, by clause 2 or the back condition, there is some $u \in W$ such that $Rwu$ and $uEu'$. Since $(W, R, V), w \Vdash \Box \varphi$, $(W, R, V), u \Vdash \varphi$, and by the Inductive Hypothesis, $(W', R', V'), u' \Vdash \varphi$ as required. So, we infer $(W', R', V'), w' \Vdash \Box \varphi$.

The converse direction is completely parallel but it makes use of clause 2 or the forth condition instead.

$\blacksquare$

Bisimulations are used to rule out the definability of some classes of frames.

Example

Each model of the form $(W, R, V)$ is bisimilar to some irreflexive model of the form $(W', R', V')$.

In broad outline, given a model $(W, R, V)$, we will build a model $(W', R', V')$, which replace each reflexive world $w\in W$, that is, each world that is accessible from itself, with a pair of duplicate worlds $w^+$ and $w^-$ in $W'$, which are accessible from each other by $R'$ but such that none of them is accessible from itself by $R'$. We then proceed to make sure that for each propositional variable $p$, each duplicate $w^+$ and $w^-$ is a member of $V'(p)$ if $w \in V(p)$ in the original model. Otherwise, $R'$ and $V'$ behave exactly like $R$ and $V$ in the original model.¹

It is not difficult to verify that $(W, R, V)$ is bisimilar to $(W', R', V')$, which means that they verify exactly the same formulas. This is because the relation $E$, which relates each reflexive world $w \in W$ with its duplicates $w^+$ and $w^-$ in $W'$ and relates every other world $u\in W$ with itself is a bisimulation between the two models.

Proposition 6.7 (Modal Undefinability for Irreflexive Frames) No formula of $\mathcal{L}^\Box$ modally defines the class of irreflexive frames.

Proof. No formula $\varphi$ of $\mathcal{L}^\Box$ is valid in all and only irreflexive frames. For suppose $\varphi$ is valid only in irreflexive frames. That means that if $R$ is not irreflexive on $W$, then there is some model $(W, R, V)$ based on $(W, R)$ such that $(W, R, V) \nVdash \varphi$. Then, given our previous observation, there is a bisimilar irreflexive model $(W', R', V')$ where $(W', R', V') \nVdash \varphi$. But notice that since $(W', R', V')$ is based on an irreflexive frame $(W', R')$, we conclude that $\varphi$ is not valid in all irreflexive frames.

$\blacksquare$

We will now argue that no formula $\varphi$ of $\mathcal{L}^\Box$ defines the class of universal frames $(W, R)$, that is, frames in which $R$ is universal on $W$, that is, for all $w,u\in W$, $Rwu$.

First, a lemma:

Lemma 6.1 A formula $\varphi$ of $\mathcal{L}^\Box$ is valid in all universal frames $(W,R)$ iff $\varphi$ is valid in all equivalence frames $(W,R)$ in which $R$ is an equivalence relation on $W$.

Proof. Given a formula $\varphi$, we look at each direction in turn:

If $(W, R)\models \varphi$ for all equivalence frames $(W,R)$, then $(W, R)\models \varphi$ for all universal frames $(W,R)$.

The contrapositive of this conditional is an immediate consequence of the observation that a universal relation $R$ on $W$ is reflexive and euclidean on $W$. So, if $R$ is universal on $W$, then $R$ is an equivalence relation on $W$. But then, if $(W, R, V)\nVdash \varphi$ where $R$ is the universal relation on $W$, then $(W, R, V)\nVdash \varphi$ where $R$ is an equivalence relation on $W$.
If $(W, R)\models \varphi$ for all universal frames $(W,R)$, then $(W, R)\models \varphi$ for all equivalence frames $(W,R)$.

We set out to show the contrapositive. That is, if $\varphi$ is not valid in all equivalence frames, then $\varphi$ is not valid in all universal frames. Suppose $(W, R, V) \nVdash \varphi$, where $R$ is an equivalence relation on $W$. We set out to find a model $(W', R', V')$ where $R'$ is a universal relation on $W'$ and $(W', R', V') \nVdash \varphi$. Since $(W, R, V) \nVdash \varphi$, there is some $w\in W$ such that $(W, R, V), w \nVdash \varphi$. Now:
$W' = \{u\in W: Rwu\}$
$R' = R \cap (W' \times W')$
$V'(p) = V(p) \cap W'$

That is, we let $W'$ consist of the equivalence class corresponding to $w$, $[w]_R$, and we let $R'$ and $V'$ be the restriction of $R$ and $V$ to that equivalence class.

A simple induction over the complexity of formulas reveals that for every formula $\varphi$

\[ \begin{array}{lll} (W, R, V), w \Vdash \varphi & \text{iff} & (W', R', V'), w' \Vdash \varphi \end{array} \]

$\blacksquare$

Corollary 6.1 No formula $\varphi$ of $\mathcal{L}^\Box$ modally defines the class of universal frames.

Proof. Suppose $\varphi$ is valid in all universal frames. Then by the former proposition, $\varphi$ is valid in all equivalence frames $(W, R)$ where $R$ is an equivalence relation on $W$. Since some of those frames are not universal frames, $\varphi$ is not valid only in universal frames.

$\blacksquare$

Much of the interest of validity in the class of universal frames is that they seem particularly suited for the evaluation of modal formulas when the modal operator is interpreted in terms of metaphysical necessity. Since the logic of universal frames coincides with that of frames in which the accessibility relation is a relation of equivalence, we appear to have reason to accept the validity of substitution instances of each of the formulas we considered above:

	Formula	Condition on $R$
$\textsf{T}$	$\Box p \to p$	reflexive on $W$
$\textsf{B}$	$p \to \Box \Diamond p$	symmetric on $W$
$\textsf{4}$	$\Box p \to \Box \Box p$	transitive on $W$
$\textsf{5}$	$\Diamond p \to \Box \Diamond p$	euclidean on $W$

Yet, some have offered reason to resist this picture of metaphysical modality.

In (Chisholm 1967) and (Chisholm 1973), Roderick Chisholm invites one to consider a ship built from one-hundred wooden planks with a tolerant essence in that the ship could have survived the replacement of one plank with a new one even if not the replacement of every plank with a new plank. That is, it is part of the essence of the ship that it can survive the replacement of a single plank whenever it exists.

One is now asked to consider a chain of possibilities, which starts with the original ship and where each possibility differs from the next just by the replacement of a single plank.

$S$	$S_1$	$S_2$	$S_3$	$\cdots$	$S_{100}$
$@$	$w_1$	$w_2$	$w_3$	$\cdots$	$w_{100}$

The paradox of tolerant essence arises when we combine what would otherwise seem reasonable thoughts:

Each pair of successive possible worlds contain the same ship, since by hypothesis, the ship’s essence tolerates the replacement of one plank with a new one.
By the transitivity of identity, $S$ is the same ship as each of the ships $S_n$ in the series. So, if it is possible for the ship to survive the replacement of two planks, then it is possible for the ship to survive that of three planks, etc.
$S$ is not the same ship as $S_100$ as they have no planks in common. It is not possible for the ship to survive the replacement of all planks.

Chisholm is inclined to reject the hypothesis that the ship has a tolerant essence: if it is essential to it to be made of the original planks, then there is no reason to even think that successive worlds in the series contain the same ship. One may alternatively attempt to blame vagueness for the problem. Maybe there comes a point at which it is indeterminate whether the original ship has survived the replacement of a given number of planks.

But the real problem is not due to vagueness. In (Leslie 2011), Sarah Jane Leslie proposes to consider an axe made from three parts: a blade, a shaft, and a handle, and to assume that the essence of the. axe is tolerant to the change of one of those three parts. We are now asked to consider a chain of just four worlds each containing an axe made from three parts, where each axe differs only by one part from an adjacent axe, and the original axe is contained in the first world. That is, the original axe is $B_1 + S_1 + H_1$:

$B_1 + S_1 + H_1$	$B_2 + S_1 + H_1$	$B_2 + S_2 + H_1$	$B_2 + S_2 + H_2$
$@$	$w_1$	$w_2$	$w_3$

The paradox now arises when we note:

Each pair of successive possible worlds contain the same axe, since by hypothesis, the axe’s essence tolerates one-part changes.
By the transitivity of identity, $B_1 + S_1 + H_1$ is the same axe as $B_2 + S_2 + H_2$. So, it is possible for the firts axe to be made of $B_2$, $S_2$, and $H_2$.
$B_1 + S_1 + H_1$ is not the same axe as $B_2 + S_2 + H_2$ as they have none of their parts in common. So, it is not possible for the firts axe to be made of $B_2$, $S_2$, and $H_2$.

Vagueness appears to play no role in this formulation of the problem. Nathan Salmon has used the first formulation of the paradox in (Salmon 1989) to argue against the validity of $4$ when $\Box$ is read in terms of metaphysical modality. His thought is to deny that what is possible with respect to $w_2$ is automatically possible with respect to $w_1$. Consider the four propositions: \[ \begin{array}{lll} p_1 & & \text{Axe is made from} \ B_1, S_1, H_1\\ p_2 & & \text{Axe is made from} \ B_2, S_1, H_1\\ p_3 & & \text{Axe is made from} \ B_2, S_2, H_1\\ p_4 & & \text{Axe is made from} \ B_2, S_2, H_2\\ \end{array} \] Then:

$p_4$ is true at $w_4$
$p_3$ and $\Diamond p_4$ are true at $w_3$
$p_2$ and $\Diamond p_3$ and $\Diamond \Diamond p_4$ are true at $w_2$
$p_1$ and $\Diamond p_2$ and $\Diamond \Diamond p_3$ and $\Diamond \Diamond \Diamond p_4$ are true at $w_1$

There is no paradox, though we would have one if we accepted every substitution instance of the formula: \[\tag{4$^\Diamond$} \Diamond \Diamond p \to \Diamond p \] For we we would be in a position to hold $\Diamond p_4$ is true at $w_1$, which would be paradoxical. As it turns out, however, ($4^\Diamond$) is equivalent to (4) above.

Example 6.1 is a special instance of this. We start with a reflexive model $(W, R, V)$ and find an irreflexive model that is bisimilar to it.↩︎

	Formula	Condition on \(R\)
\(\textsf{T}\)	\(\Box p \to p\)	reflexive on \(W\)
\(\textsf{B}\)	\(p \to \Box \Diamond p\)	symmetric on \(W\)
\(\textsf{4}\)	\(\Box p \to \Box \Box p\)	transitive on \(W\)
\(\textsf{5}\)	\(\Diamond p \to \Box \Diamond p\)	euclidean on \(W\)

	Formula	Condition on \(R\)
\(\textsf{T}\)	\(\Box p \to p\)	reflexive on \(W\)
\(\textsf{B}\)	\(p \to \Box \Diamond p\)	symmetric on \(W\)
\(\textsf{4}\)	\(\Box p \to \Box \Box p\)	transitive on \(W\)
\(\textsf{5}\)	\(\Diamond p \to \Box \Diamond p\)	euclidean on \(W\)

Frames	Modal Definability	First-Order Definability
Reflexive	\(\Box p \to p\)	\(\forall x \ Rxx\)
Symmetric	\(p \to \Box \Diamond p\)	\(\forall x \forall y (Rxy \to Ryx)\)
Transitivity	\(\Box p \to \Box \Box p\)	\(\forall x \forall y \forall z (Rxy \wedge Ryz \to Rxz)\)
Euclidean	\(\Diamond p \to \Box \Diamond p\)	\(\forall x \forall y \forall z (Rxy \wedge Rxz \to Ryz)\)

	Formula	Condition on \(R\)
\(\textsf{T}\)	\(\Box p \to p\)	reflexive on \(W\)
\(\textsf{B}\)	\(p \to \Box \Diamond p\)	symmetric on \(W\)
\(\textsf{4}\)	\(\Box p \to \Box \Box p\)	transitive on \(W\)
\(\textsf{5}\)	\(\Diamond p \to \Box \Diamond p\)	euclidean on \(W\)